単回帰 数式を使った理解編
挨拶&はじめに
こんにちは。キノコードです。
前回の「ゼロからわかる単回帰分析」はみていただけましたでしょうか?
前回の動画で予告した通り、ゼロからわかる単回帰分析の次は、「数式を使って理解編」です。
つまり、数学・統計学を使って概念の説明していきます。
中学、高校に習った数学なども出てきます。
中学、高校の頃は、「数学なんて大人になってから使わないでしょ。なんのために勉強しているのかわからない」と思ったことありませんか?
そうです。こういったところで使われるのです。
僕自身は「もっと真剣に勉強しておけばよかったなー」と10年ぐらいに思いました。
でも、何かを始めるには遅いすぎるなんてことはないです。
今から始めていれば1年後には、1年の経験者ですから。
キノコードでは、人工知能のレッスンの他に、データ可視化のレッスン、Pythonを使った仕事の自動化のレッスンを配信しています。
他にも、これからはWebアプリケーション開発の動画や、データ分析に必須のSQLの講座も配信していく予定です。
新着通知がいきますので、ぜひチャンネル登録をお願いします。
それでは、レッスンスタートです。
単回帰分析とは(前回動画の復習)
数学を使った理論の説明する前に、前回の動画の内容を簡単に復習します。
前回のレッスンでは、回帰分析は「部屋の数からマンション価格を予測する」などといった量的データの予測に使用される手法だと説明しました。
量的データとは、駅までの距離やマンション価格のように数字で表現でき、各データの大きさが比較できるデータのことです。
一方、質的データとは、男性や女性などの性別、A型B型などの血液型のように各データの大きさが比較できないデータのことです
また、回帰分析では、予測に使用するデータを説明変数、予測したいデータを目的変数といいます。
この説明変数・目的変数には別名もありますが、この動画では説明変数・目的変数という用語を使用します。
先ほど紹介した、部屋の数からマンション価格を予測する例では、部屋の数が説明変数で、マンション価格が目的変数です。
しかし、部屋の数だけでマンション価格を予測するのは難しいです。
マンション価格するには、例えば、部屋の数のほかに、部屋の広さ、駅までの距離、築年数なども説明変数に使えそうです。
したがって、予測に使う説明変数が一つの場合は、今回ご紹介する単回帰分析。
説明変数が二つ以上になる場合は、重回帰分析と言う名称になります。
そして、この動画では、単回帰分析についてご説明しています。
また、重回帰分析について、別途、動画を作りますので、チャンネル登録をしてお待ちいただければと思います。
さて、単回帰分析の復習に戻ります。
単回帰分析とは、わかりやすく言い換えると、「データの中心を通る直線から、目的変数を予測する手法」といえます。
では、データの中心を通る直線とはどういうものでしょうか。
まずは、表示されている図をご覧ください。

横軸は部屋の数。右にいけばいくほど部屋の数が多いとします。
縦軸がマンションの価格。上にいけばいくほどマンション価格が高くなるとします。
Aマンションがこれ、Bマンションがこれ、Cマンションがこれ、といったような形でデータをプロットをしています。
前回のレッスンでは説明しませんでしたが、このように、部屋の数とマンション価格といったような1組のデータに対応する点をプロットしたものを散布図といいます。
散布図は、マンション価格と駅までの距離、マンション価格と部屋の広さ、マンション価格と築年数といった、2つのデータの関係性を見るのによく使用されます。
データ分析ではよくつかわれるデータ可視化の技術なので、ぜひおぼえておきましょう。

データの中心を通りそうな直線をひいてみるとこのようになると思います。
直線をひいてみると明らかになりますが、部屋の数が多ければ多いほどマンションの価格があることがわかってきます。
でも、これはデータの中心を通りそうな直線であって、勘でひいていたのでは、人によって予測する直線がずれる問題が生じます。
この人によって予測する直線がずれる問題を解決してくれる手法が最小二乗法です。
最小二乗法は簡単に言えば、数式で「点の集まり、つまり各点の中心を通る直線」を決める手法です。
また、最小二乗法で引いた直線を回帰直線といいます。
ここまが前回のレッスンの復習です。
最小二乗法の数式的説明
それではここから、最小二乗法がどのようにして「各点の中心を通る直線」を定義しているのかを数式を使ってご説明します。
前回の動画では、「各点の中心を通る直線」とは、「各点からY軸に平行な直線を引き、その距離を2乗した値の合計が最も小さくなる直線」という説明をしました。
言葉では、よくわからないと思いますので、グラフを使用しながら順番に説明していきます。

このグラフは、3組のデータと私が直感的に引いた中心を通る直線です。
3組のデータ、つまり、各点の座標を、(x1,y1),(x2,y2),(x3,y3)とします。
この3組のデータの中心を通る直線が数式でどのように定義されるかみていきましょう。
中学校で習った直線の数式の復習をします。
まず、直線は、yイコール、axプラスbという数式で表せます。
この直線の式で、bをなんというか覚えていますか。
答えは切片です。
切片は、グラフのxイコール0の時のyの値のことです。
この、yイコール、axプラスbという数式で、2次元上の全ての直線を描くことができます。
2次元とは、x軸とy軸といったように、2つの軸があるものと考えてもらって良いです。
3次元とは、x軸とy軸とz軸の3つの軸があるということです。
3次元まであると、平面ではなく、立体になりますよね。
さて、2次元上にかかれた直線を描くには、aとbを求めれば描くことができます。
ここは、数学に慣れていない方には、少しイメージしにくい説明かもしれません。
ですが、とにかくここでは、2つだけ覚えておいてください。
直線の方程式は、yイコール、axプラスbである。
直線を求めるというは、aとbの値を決めることである。
この2つを覚えておいてください。
さて、最小二乗法は、各点の中心を通る直線、つまり、回帰直線を求める手法だと説明しました。
そして、回帰直線は、回帰直線のaとbを求めることができれば描くことができます。
つまり、回帰直線を求めるとは、散布図にプロットしたような各点からaとbを求める手法ということになるのです。
ここは、重要なので覚えておいてください。
回帰直線を求める方法をぼんやりイメージできましたでしょうか?
では、具体的にはどうやって求めるのでしょうか?
もう1度復習しますが、回帰直線は、「各点の中心を通る直線」であり、「各点からY軸に平行な直線を引き、その距離を2乗した値の合計が最も小さくなる直線」という説明をしました。

表示されている数式では、aとbの代わりにそれぞれ、w0、w1という文字を使用しています。
これは、機械学習の分野では、aやbのような定数を、重み、英語で言うと、weightの頭文字のwという文字が使用されることが多いためです。
また、他にも、機械学習の分野で、yイコールw1かけるxプラスw0という表記より、yイコールw0プラスw1かけるxと表記されることが多いのでその順番で書き記しています。
直線のyの上についている三角のマークは、「ハット」と読み、「yハット」というように読みます。
このハットは、主に、推定量を表す記号として使用されています。
推定量とは、厳密な定義とは少し異なりますが、ここでは、推定される値、つまり、予測される値、予測値と考えてください。
確かに、yハットは3点か予測値なので、ハットをつけて表現されるのはおかしくないですよね。

次に、英語の大文字Eのような記号について説明します。
これはギリシャ文字で、ε(イプシロン)といいます。
ちなみに、機械学習の世界や数学の世界では、文字を英語ではなく、ギリシャ文字で表現ことが多いです。
さて、ε(イプシロン)とは図で示しているように、各点から直線まで距離、各点のyの値とyハットとの距離です。
先ほどの表現で言えば、イプシロンは、「各点から予測した直線まで引いた線のそれぞれの距離」になります。
このイプシロンのことを、数学的には残差といいます。
さて、こまめに復習をしていきます。
回帰直線の求め方は、「各点からY軸に平行な直線を引き、その距離を2乗した値の合計が最も小さくなる直線」という説明をしました。
勘のよい方は気づい方かもしれません。
「各点からY軸に平行な直線を引き、その距離」、これが残差のことです。
この「残差を2乗した値の合計が最も小さくなる直線」が回帰直線なのです。
では、なぜ、各点から直線の距離、つまり、残差を2乗するのでしょうか。
これは、値の符号を全てプラスにしたいからです。
例えば、2乗をせずに、そのまま合計をしたらどうなるでしょうか?
直線より上にある点はプラスですが、直線より下ある点はマイナスになります。
つまり、ここがプラス4、ここがマイナス3、ここがプラス1だったとすると、足し合わせると2になってしまいます。
したがって、2という距離になり、これはイプシロン1より短くなってしまいます。
これでは、距離の合計には、ならないですよね。
そこで、この問題を解決するアイデアとして、残差の絶対値を取ることが考えられました。
絶対値というのは、簡単にいうと、値がマイナスの場合はそのマイナスを消してプラスにした値と思っていただければよいです。
絶対値の合計であれば、マイナスの値は出てこないので、しっかりと各点までの線の距離の合計が求められます。
例えば、先程の例で言うと、プラス4、ここがマイナス3、ここがプラス1だったとすると、その絶対値の合計は、8ですよね。
これだと正しい残差が求められそうです。
この絶対値を使用した回帰分析は、最小絶対値法といいます。
しかし、絶対値は、数学的に扱い辛い処理になります。
数学的に扱い辛いというのは、詳しい説明を避けますが、微分がし辛いという認識でよいと思います。
なので、最小二乗法では、代わりに残差を2乗する方法で、マイナス量がでないようにしているのです。
ちなみに、2乗は自乗ともいいますので、最小自乗法という場合もあります。

最小二乗法のイメージはつきましたか?
もう1度復習をします。
最小二乗法は、回帰直線を求める手法であり、回帰直線は、「残差を2乗した値の合計が最も小さくなる直線」です。
つまり、イプシロンの2乗が最も小さくなる直線を求めればいいですよね。

この各点までの線の距離、つまり残差のイプシロンはグラフの数式では、yひくyハットとなります。

yハットに方程式の右辺を代入すると、このようになります。

ごちゃごちゃしてきたので、式のみ表示させてみましょう。
この部分を大文字のS、添字にイプシロンの1、ほかも同様の文字に置き換えます。

これを縦に並べます。

そして、足し算します。
高校の頃に習いましたが、足し算はシグマで表現できます。
シグマとは、全てを足し合わせるという意味です。
シグマは、イメージとしては、エクセルでSUM関数を使用していると思っていただければ良いです。
これで、「残差を2乗した合計」を数式で表すことができました!
ちなみに、残差を2乗した合計のことを、残差の二乗和といいます。
また、二乗和は別名、平方和ともいいます。
こられも合わせて覚えておきましょう。
さて復習をします。
ここまでみてきたように、最小二乗法の短い説明としては、残差の二乗和を最小にするw0とw1を見つける手法と説明できます。
つまり、(x1,y1)、(x2,y2)、(x3,y3)は、実際は、(2,10)(5,12)(8,14)といったように与えられています。
そして、予測する直線は、傾きと切片がわかれば描くことができます。
つまり、w0とw1がわかれば、直線を描けます。
そして、与えられた各点から残差の二乗和を最小にする、w0とw1を求めることができれば回帰直線を描けます。
もう一度いうと、最小二乗法は、残差の二乗和を最小にするw0とw1を見つける手法ということです。
理解できましたでしょうか?
残差の比較
ここまでの話を整理し、理解を深めるために次のような問題について考えてみます。
次のグラフをご覧ください。

見ての通り、3組のデータの散布図に2本の直線が描かれています。
赤色の直線は「y = 2 x + 3」
青色の直線は、「y = 3 x」
では、この2本の直線のうち、どちらの方が、3点の中心に近い直線なのでしょうか。
中心に近い直線というは、残差の二乗和が小さい方の直線のことでした。
さて、この赤色と青色どちらの方が、3点の中心に近いのか計算してみます。
まずはじめに、情報として、3点のxとyの値は、左から、(2,10),(5,12),(8,14)です。
また、赤色直線は、言い換えたをかえると、yハット、イコール、3プラス、2、かけるxの直線です。
青色が、yハット、イコール、3、かける、xの直線です。
では、それぞれ先ほど説明したやり方で残差の二乗和、エスの合計値を計算してみましょう。
せっかくなのでpythonで計算してみます。
#1点目(x,y)=(2,19)からの残差
S1 = (10 - (3 + 2*2))**2
print(S1)最初は赤色直線の残差の二乗和を求めてみます。
コード部分にあるように、赤色直線のw0とw1の値は、それぞれ、w0が3、w1が2です。
これを1点目のxが2、yが10の時のエス1は、値を該当するところに代入して、計算すると9となります。
これを2点目、3点目も同様の計算をして、エス2、エス3の計算も行います。
最後に、赤色直線の合計を、エス、アンダーバー、レッド、アンダーバ、サムという変数に代入しておきます。
#1点目(x,y)=(2,10)からの残差
S1 = (10 - (0 + 3*2 ))**2
#2点目(x,y)=(5,12)からの残差
S2 = (12 - (0 + 3*5))**2
#3点目(x,y)=(8,14)からの残差
S3 = (14 - (0 + 3*8))**2
S_blue_sum = S1 + S2 + S3青色の場合も同様に、青色直線の残差の二乗和を、エス、アンダーバー、ブルー、アンダーバ、サムという変数に代入しておきます。
("赤色",S_red_sum)
print("青色",S_blue_sum)それでは、両方の値を出力して比較してみましょう。
結果は、赤色直線、35、青色直線、125と、赤色直線の方が、青色直線より中心に近い直線という結果になりました。
確かに、ぱっと見、各点からと直線の距離は、赤色直線の方が近そうに見えます。
したがって、この計算が、直感的にも正しいことがわかります。
さて、このように、直線が2本与えられ、そのどちらの方が、中心に近いのかの計算方法はわかりました。
ですが、最終的に知りたいのは、この先ほど求めた残差の二乗和が最も小さくなる時の、w0とw1です。
これを求めるのには、どうすればよいのでしょうか。
簡単な微分の説明
ここで、使用するのが微分です。
高校のときに習いましたが、微分は最小値や最大値を求めることができる処理です。
どのように求めるのか簡単に説明します。
まず、微分は、簡単にいうと、関数の傾きを求める処理です。
yイコール、xの2乗の関数を使用して説明します。
#微分説明用の図
from matplotlib import pyplot as plt
plt.figure(figsize=(12, 8))
xdata = np.linspace(-2, 2)
ydata = [_**2 for _ in xdata]
plt.plot(xdata, ydata, 'b')
plt.xlim(-2,2)
plt.show()表示されているのが、yイコール、xの2乗の関数のグラフです。
このグラフでyが最も小さい値になるのは、xの値がいくつの時でしょうか。
視覚的にわかると思いますが、xが0の時、yが最も小さい値になっています。
これを微分では、どのように求めているのでしょうか。
先ほど、微分は傾きを求める処理だといいました。
傾きとは何でしょうか。
傾きは、xの増加量分のyの増加量で定義されています。
この傾きですが、傾きが0に近づくほど、yの最小値に近づくいう性質があります。
具体的に、0から1の傾きと1から2の傾きを求めて見ましょう。
両方とも、xの増加量分は1、yの増加量も1です。
したがって、xの0から1の傾きは、1ぶんの1で、1です。
次に、xが1から2の時の、yの増加量は、xが1の時、yは1、xが2の時、y4なので、yの増加量は3です。
したがって、xの1から2の傾きは、1ぶんの3で、3です。
つまり、xの0から1の傾きは1、xの1から2の傾きは3です。
yの最小値は0です。
xの0から1と、xの1から2の区間では、0から1の区間の方が、yの最小値に近いです。
実際に、0から1の区間の方が、傾きは小さいです。
つまり、ここからわかる通り、傾きが0に近づくほど、yの最小値に近づくいう性質があります。
この傾きですが、xの区間を今の0から1ではなく、0から0.5、0から0.1とだんだんと小さくして考えることもできます。
この区画を限りなく小さくしていくと、区画ではなく、ほぼ、xの値に対しての傾きを求めることができます。
そして、このxの値に対する傾きが0になる点こそ、yの最小値を取ることが知られています。
また、このxの区間を限りなく小さくするという処理が、微分なのです。
つまり、微分して0になるxの値を求めれば、yの最小値を求めることができるのです。
では、実際に微分で、yの最小値を取る、xの値をyイコールxの2乗の関数から求めてみましょう。
xの2乗を、微分すると、2xになります。
微分の計算方法については、ここでは解説しません。
微分について説明して欲しい方がいればぜひコメントください。
そちらも動画で解説動画を作りたいと思います。
微分の計算方法がわからない方は、今はそうなるだと思っていただければ結構です。
そして、微分して傾きが0になる時のxが最小値をとるxです。
ですので、0イコール2xという方程式を解きます。
両辺を2で割り、xイコール0という値が得られます。
微分から、yイコール、xの2乗の最小値を取るxは0という結果が得られました。
求めらえたxの値0を元のyイコール、xの2乗のxに代入すると、yの最小値が得られます。
代入すると、yイコール、0の2乗になるので、yイコール0、グラフから読み取った最小値と同じ値が得られました。
微分のイメージ的な説明
ここまで、微分について説明してきましたが、やっぱりよくわからないという方向けのとっておきの説明があります。
微分は傾きを求める処理だと説明しましたが、もう一つイメージ的な説明があります。
それは、微分とは、ボールが止まる位置を探す処理である。
というものです。
先ほどの、グラフをもう一度見てください。
ここに、ボールを転がしたらxのどこで止まるでしょうか。
最終的には、xイコール0のところでボールが止まると考えられます。
とにかく、数式的にはよくわからないという方は、この微分はボールが止まる位置を探しているというのを意識してみてください。
そして、ボールが止まる位置の傾きは0であるということも合わせて覚えておきましょう。
最後に、ここまでの微分の説明はわかりやすさを重視しているため、細かい部分に齟齬があることはお伝えしておきます。
残差の合計が一番短いところを求める
さて、微分についての説明が長くなってしまいました。
ですが、私たちが今取り組んでいる問題は、残差の二乗和を最小にすることです。
そして、先ほどエスを使用して、残差の二乗和を数式で表すところまではできています。
最後に、微分の知識も使用して、残差の二乗和が最も小さくなる時の、w0とw1を求めたいと思います。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Figureと3DAxeS
fig = plt.figure(figsize = (10, 10))
ax = fig.add_subplot(111, projection="3d")
# 軸ラベルを設定
ax.set_xlabel("w0", size = 16)
ax.set_ylabel("w1", size = 16)
ax.set_zlabel("S", size = 16)
w0 = np.linspace(-50, 50, 20)
w1 = np.linspace(-10, 10, 20)
w0, w1 = np.meshgrid(w0, w1)
# 変換
w0 = np.array(w0)
w1 = np.array(w1)
#残差の二乗和を求める
S_sum = (10 - (w0 + w1*2 ))**2 + (12 - (w0 + w1*5))**2 + (14 - (w0 + w1*8))**2
# 曲面を描画
ax.plot_surface(w0, w1, S_sum, cmap = 'bone')
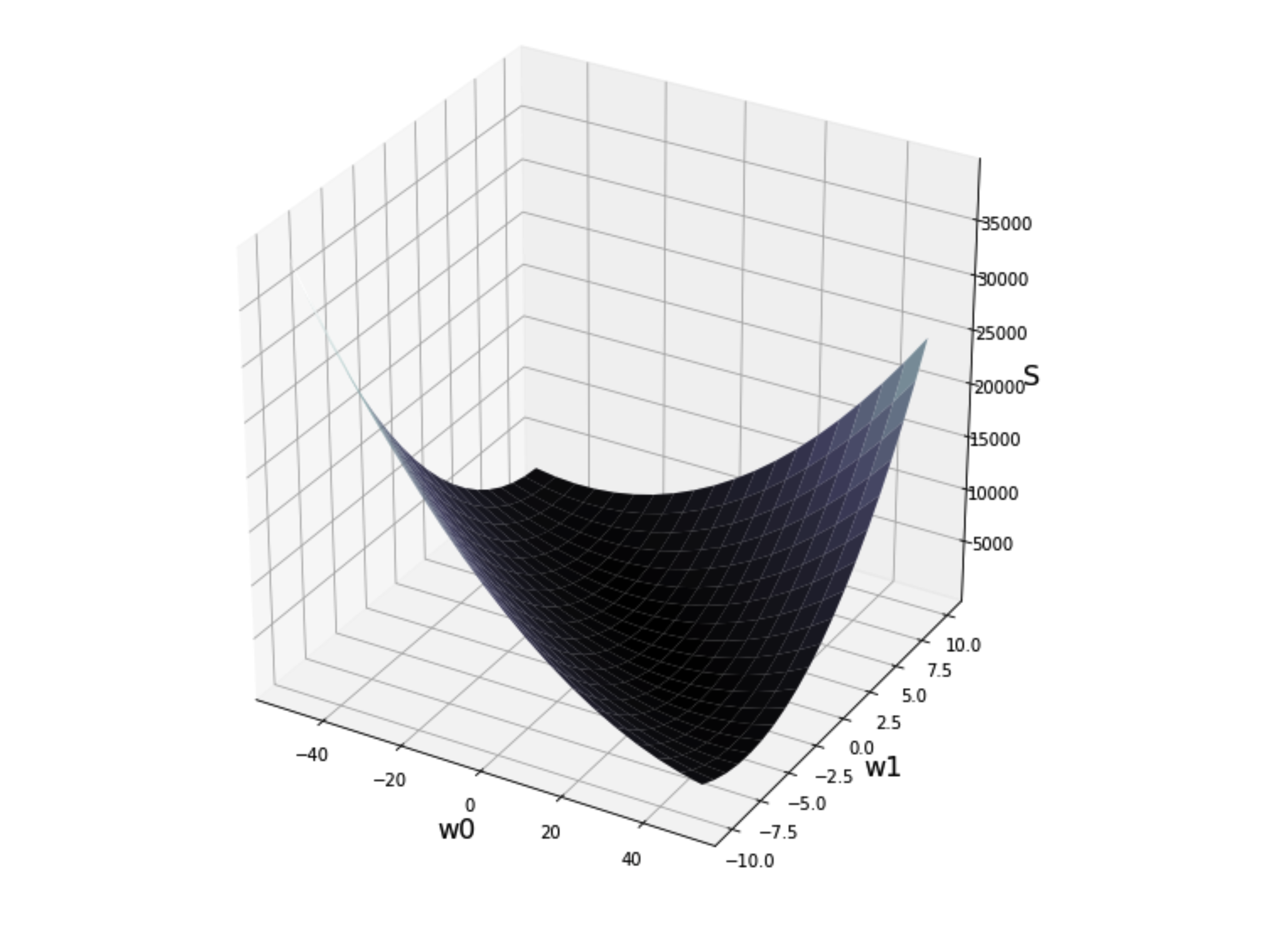
plt.show() 残差の二乗和の式は、w0とw1が変数になるため、このような3次元のグラフになります。
この、曲面の一番底のところが最小値、つまり、残差の二乗和が最も小さくなるw0とw1の組み合わせということになります。
ここで、先ほどの微分のイメージ、ボールの話を思い出してください。
この曲面にボールを転がすと、一体どの辺で止まるでしょうか。
w0とw1の軸に対して斜めに入っているどこかの谷で止まりそうです。
このボールが止まる位置、つまり傾きが0のところが最小値というのは3次元の曲面でも変わりません。
先ほどの、yイコールxの2乗のグラフでは、視覚的にどこが最小値がすぐにわかりました。
ですが、この曲面だと、斜めの谷のどこかというところまでしかわかりません。
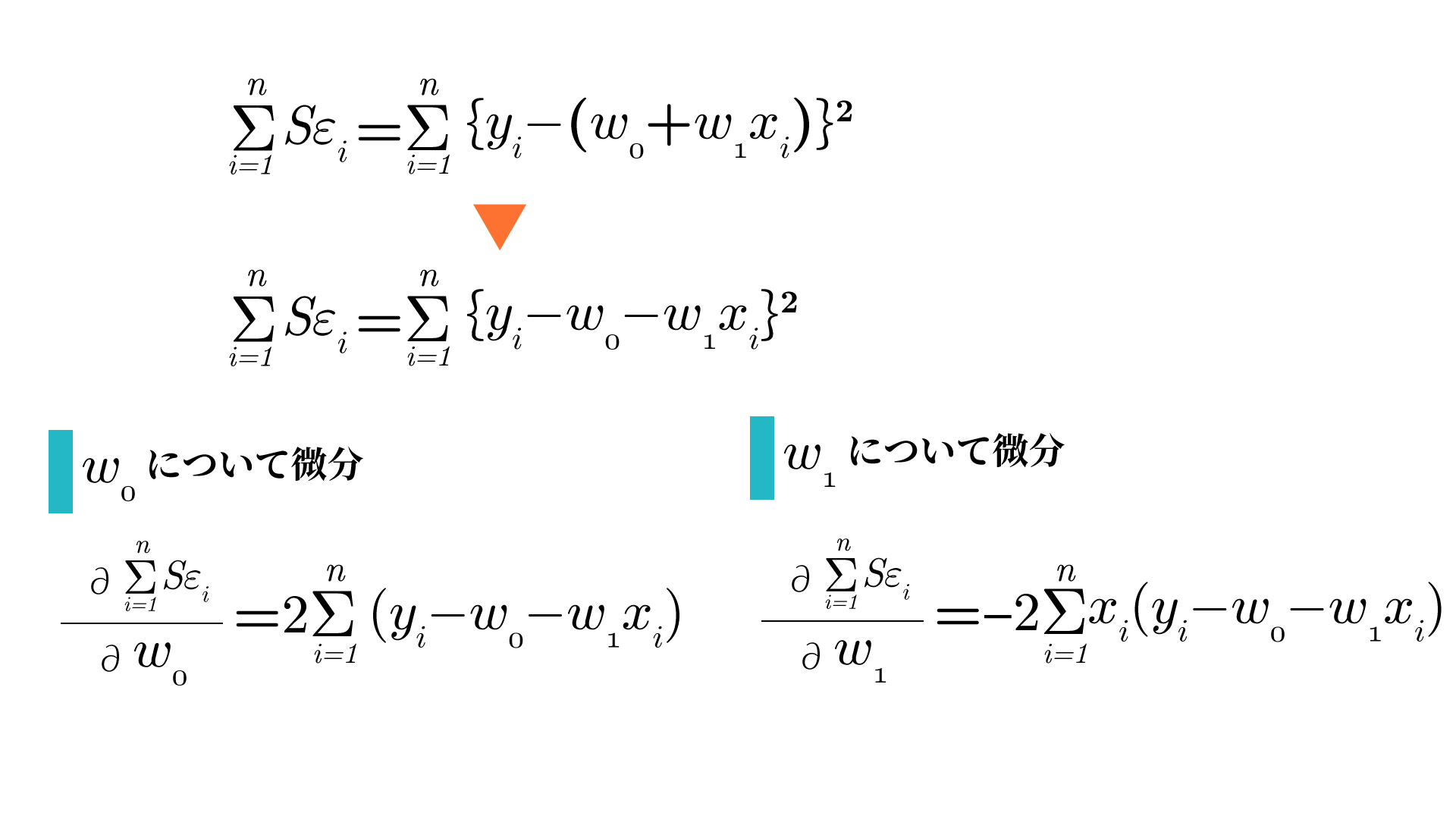
そこで、ここで微分をして数式的に解いていきます。
このような曲面の最小値を求める処理は、正確には微分ではなく、偏微分という手法で解きます。
偏微分は、理系の大学1年生で習います。
偏微分の詳細な説明は、ここでは行いません。
ですが、偏微分の計算手法は、微分と対して変わりません。
片方の変数を定数とみて、微分をすれば良いだけです。
また、大雑把な理解ですが、偏微分は微分の例と同じく、曲面でボールが止まる位置を探している処理を思っていただければ結構です。
まず、w0とw1に対してそれぞれ偏微分を行います。
w0とw1に対して偏微分を行い、出てきた関数は傾きを表す関数です。
ですので、偏微分をして出てきた関数をイコール0で繋ぎます。
そうすると、w0が傾き0の場合、w1が傾き0の場合を求めることができます。
そして、その2つの式を、連立方程式で解いていきます。
その連立方程式をw0とw1について解くと最終的に次のような形になります。

この式で求められたw0とw1こそが、最小二乗法によって求められた、w0とw1ということになります。
import numpy as np
x = [2,5,8]
y = [10,12,14]
w1, w0 = np.polyfit(x, y, 1)
print(w1, w0)それでは、Pythonを使って、w0とw1を求めてみましょう。
この、w0とw1はナムパイの、polyfitメソッドを使用をして求めることができます。
引数に、xとyのリスト、最後に、次数を渡します。
今回は、1次関数なので、最後の引数は1になります。
また、返り値が、w1、w0、2つかえって来るので、二つの変数を用意しておきます。
xの係数、切片の順で返ってくるので、w1、w0の順で記述しています。
from matplotlib import pyplot as plt
plt.figure(figsize=(12, 8))
xdata = list(range(10))
ydata = [i*w1 + w0 for i in xdata]
plt.scatter(2,10)
plt.scatter(5,12)
plt.scatter(8,14)
plt.xlim(0,10)
plt.ylim(0,25)
plt.plot(xdata, ydata, 'r')それでは、求められたw1、w0とデータをグラフで表示して見ます。
求められた、w1とw0の直線がデータによくフィットしていることがわかります。
ちなみに、全ての点に直線が重なるほど、精度がよくなっています。
今回は、全ての点に直線が重なっています。
データによっては点が直線に乗らないこともたくさんあることを補足しておきます。
このように、回帰直線を求める方法が最小二乗法です。
回帰直線さえ求めることができれば、予測することが可能になります。
単回帰分析、回帰直線、最小二乗法と色々用語がでてきたので整理をします。
単回帰分析は、説明変数が1つの回帰分析を指します。
前のレッスンでもお伝えしましが、回帰分析とは、予測分析と読み替えてしまってよいです。
最小二乗法とは、各点の中心を通る直線を求める手法です。
そして、各点の中心を通る直線のことを回帰直線といいます。
ご理解いただけましたでしょうか?
線形回帰の精度評価方法、相関係数、決定係数
最後に、単回帰分析の予測の精度を評価に使用する係数について紹介します。
単回帰は、身長から体重を予測、駅までの距離でマンション価格を予測するなど、あるデータからあるデータを予測するための手法だと説明しました。
したがって、単回帰分析をすれば予測することができます。
単回帰分析で予測をすることはできますが、予測の精度が高いか低いかは別問題です。
そのため、単回帰分析をした結果の予測精度がどれぐらいなのかを知ることは重要です。
単回帰の精度評価には、主に相関係数と決定係数という係数が使用されます。
相関係数は、-1から1までの値をとります。
決定係数は、0から1までの値をとります。
また、決定係数は相関係数を2乗した値です。
相関係数と決定係数については、視覚的に見た方が直感的に理解できますので、次の画像をご覧ください。
スライドに示すように、決定係数が高ければ高いほど、データの散らばりは小さくなります。
決定係数が1であれば、全ての点が回帰直線と重なっている状態になります。
先ほど、決定係数は相関係数を2乗した値だと説明しました。
こんな単純な数学的な処理をするだけなら相関係数・決定係数はどちらか一つでも良いのではないか。
と思われるかもしれません。
しかし、相関係数と決定係数の値は似ていますが、意味することが微妙に異なります。
まず、決定係数は回帰直線の当てはまり度合いの指標です。
0であれば、回帰直線にデータは全く当てはまらない。
1であれば、先ほど説明したように、データが全て回帰直線上にあることになります。
つまり、決定係数が1に近いほど、回帰直線、単回帰の予測精度は高いことを示しています。
それは、相関係数でも同じではないのかと思われるかもしれません。
確かに、相関係数が高ければ、決定係数も高くなるので、その見方は間違ってはいません。
しかし、相関係数は、あくまで二つのデータの相関、つまり関係性を見るための指標と考える方が正確です。
決定係数にはマイナスはありませんが、相関係数にはマイナスがあります。
これは、データの関係性には、身長が高ければ、体重も重いといった、片方のデータが大きくなればもう片方も大きくなる関係性ばかりではないためです。
例えば、貯金額と支出の相関をとれば、支出が増えれば、貯金額は減ると思いますので、相関係数はマイナスになるでしょう。
このように、相関係数には、二つのデータの関係性をみるための指標として使われます。
決定係数のPythonでの求め方についてはPython実装編にて説明をします。
エンディング
人工知能レッスン4「単回帰分析」の数式を使った理解編お疲れ様でした。
次回は、実際のデータを使用し、単回帰分析を行い、データの予測を行っていきます。
それでは次のレッスンでお会いしましょう。




