挨拶&はじめに
こんにちは、kinocodeです。
前回の「単回帰分析」の数学を使って理解編は、ご覧いただけましたか。
前回の動画までの動画は、理論の話だったので理解しづらかったところがあると思います。
今回は手を動かしながら理解を深めていきましょう。
そこで、この動画では、Excelを使って単回帰分析をしていきます。
ではなぜExcelで分析をするのでしょうか?
理由は3つあります。
1つめは、理解の観点です。
この人工知能入門講座は、Pythonで分析コードを書けることだけではなく、できるだけ数学的な理解も深めていただきたいと考えています。
その方が、深いデータ分析ができるようになりますし、理解ができれば応用が可能になります。
本や動画で学んだことはできるけど、実務になったら使えないということはありませんか?
それの要因としては、理論についての理解がまだまだ浅い状態だからです。
Excelは、Pythonとは違い、常に全てのデータが見える状態に近いです。
したがって、データの数字がどういう操作を経て分析されているかを直感的に理解でき、分析への理解が深まると考えています。
私自身、機械学習で理解が進まないときはExcelやGoogleSpreedSheetを使って計算したりしていました。
2つめは、使いやすさの観点です。
会社のパソコンにPythonはインストール不可の方もいらっしゃると思います。
だけど、Excelが使用できない会社はそうそうないと思います。
したがって、ほとんどの人が、単回帰分析をExcelを使って使いこなすことができるようになります。
分析の結果を単回帰分析とともに報告をすると、説得力が増し、上司の方から驚きや喜びの反応があるかもしれません。
3つはExcelのツールの素晴らしさです。
Pythonはプログラミングであり、ビジネスパーソンからは少し遠い存在です。
だからこそ、かっこよさがあるかもしれません。
でも、Excelは優れたツールです。
データ集計をするにも、データ分析をするにも、手軽で、みんなが使っているツールです。
私の前職でもさっと分析する際は、Excelを使ってやっている方が多かったです。
上司も使えるツールなので、歓迎されていました。
そこで、Excelのレッスンを導入した次第です。
人工知能入門講座レッスンでは、Pythonでの分析に入る前にエクセルでの分析レッスンを可能な限り行う予定です。
Excelでの分析方法もぜひマスターしてください。
キノコードでは、人工知能のレッスンの他に、データをグラフにするレッスン、データ集計・加工に関するレッスン、Pythonを使った仕事の自動化のレッスン、SQLのレッスンなどを配信しています。
他にも、これからはWebアプリケーション開発の動画なども配信していく予定です。
新着通知がいきますので、ぜひチャンネル登録をお願いします。
それでは、レッスンスタートです。
ボストンの住宅価格データセットの説明
!pip install scikit-learnまず、初めに、今回の単回帰分析で使用するデータセットについて説明します。
今回、エクセルでの分析に使用するデータは、アメリカの都市、ボストンの住宅価格に関するデータセットです。
このデータセットは、ライブラリのsklearn(サイキットラーン)に入っています。
sklearnは、色々な機械学習をすることができる便利なライブラリです。
このデータセットは、次のPython実装編でも使用するデータになります。
したがって、pip installでインストールします。
ボストンの住宅価格に関するデータセットの中身について説明します。
このデータセットは、ボストンの分割された区画のデータで構成されています。
ボストンを506の区画に分割し、それの各区画に関するデータが14項目あります。
各区画に関するデータとは、その区画の犯罪率や住宅価格の中央値などです。
データの各項目に関する詳しい情報については後ほど説明します。
このボストン住宅価格のこのデータセットは、機械学習においては有名で、
このデータは基本的に、住宅価格を目的変数、それ以外を説明変数として使用します。
つまり、住宅価格を色々なデータで予測するために使用します。
今回は、住宅価格に大きく影響しそうなデータを1つ使用して、単回帰分析をおこないます。
エクセル編では、エクセルでの操作をしやすくするために、全506個のデータから50個のデータを取り出して分析をおこないます。
それでは、必要な50個のデータをPythonで抽出し、エクセルファイルに書き出していきましょう。
ちなみに、データ抽出についてはPythonも得意ですが、もっと大量データになった場合にはSQLが便利です。
キノコードには、SQL超入門講座というレッスンもありますので、ぜひそちらもご覧ください。
ボストンの住宅価格データセットの読み込み・前処理
from sklearn.datasets import load_boston
import pandas as pdボストンデータの抽出に使用するライブラリをインポートしていきます。
まずは、sklearnの中にあるボストンデータをインポートします。
次に、取得したボストンデータをエクセルファイルに書き出すために、Pandasをインポートします。
実行します。
bs = load_boston()次に、ボストンデータをbsという変数に代入をします。
bsという変数に代入するために、bs、イコールと書きます。
次に、ボストンデータを読み込むのに、load_boston丸括弧と書きます。
実行します。
今回の操作では、データを読み込んだだけなので、何も表示されません。
bs次に、読み込んだ、ボストンデータをみて見ましょう。
print関数でbsの中身をみてみましょう。
たくさんの情報が出力されて見づらいですが、ボストンデータの中身はこのようになっています。
データは辞書型で格納されています。
上の、データの部分に、各区画の犯罪率などのデータが入っています。
次に、ターゲットの部分に住宅価格の中央値のデータが入っています。
次のフィーチャーネームに先程の、データの名称の略称が入っています。
ちなみに、最初の、CRIMが犯罪率、ZNが広さ、INDUSが産業、CHASが川の隣であるか、NOXが環境、RMが部屋数、AGEが築年数です。
次のDESCRに、このデータセットは何であるか、データの略称名の説明、リファレンスなどが入っています。
そして、最後のファイルネームに、データセットの保存場所のパスが書かれています。
また、ファイルパスから、このデータはcsv形式で保存されていることがわかります。
なお、私はAnacondaの中に入っているJupyterLabを使用しています。
Anacondaを使用していない方は、パスが書かれていないかもしれません。
print(bs.DESCR)データの情報を見るために、DESCRの中身を見やすくして表示してみましょう。
DESCRの中身を見やすくして表示するにはprint関数を使用します。
実行します。
ボストンデータに関する情報が表示されていますね。
表示されている、中央付近のアトリビュートインフォメーションに、データの属性情報が書かれています。
今回は、この中から、部屋数の平均RMと、住宅価格の中央値MEDVというデータを使用し、単回帰分析をおこないます。
なぜ、このデータを選んだかというと、部屋数と住宅価格には正の相関関係があると考えられるからです。
つまり、部屋数が多い方が、家が大きく価格も高いだろう仮説を検証することになります。
この仮説が当たっているかどうか単回帰分析でみていきましょう。
df = pd.read_csv(bs.filename, header = 1)それでは、ボストンデータをパンダスに読み込んでいきます。
先程、ご紹介したように、このデータはサイキットランの中にcsv形式で保存されています。
そこで、パンダスのリードcsvメソッドを使用して、データを読み込んで行きます。
ボストンデータを入れる、変数名をディーエフとします。
イコールと書いて、ピィディー、ドット、リード、アンダーバー、csv、括弧、1つ目の引数には、csvファイルのパスを渡します。
先程、参照したビーエスの、ファイルネームという属性に、csvファイルのパスは書かれていました。
そこで、ビーエス、ドット、ファイルネームを1つ目の引数として渡します。
これで、ファイルパスを引数として渡すことができます。
次に、ヘッダー、イコール、1を2つ目の引数として渡します。
これは、データフレームとして読み込みはじめる行数になります。
今回読み込む、ボストンデータのcsvファイルの0行目には、カラム数13と行数の506という情報が入っています。
これは、分析には使用しないので、それを読み込まずに、データフレームを作成するための記述です。
次に、読み込んだボストンデータの中身を確認するために、ディーエフと書きます。
実行します。
df = df[['RM','MEDV']]
dfここから、分析に使用するデータだけを取り出していきます。
説明変数として、分析に使用するのは、部屋数の平均が入った、RMです。
また、目的変数である、住宅価格の中央値が入った、MEDVも取り出します。
データフレームから、複数の列を取り出すには、まず、角括弧を二重に重ねます。
次に、必要なカラム名をシングルクォーテーションで括ります。
カンマを書き、再度必要カラム名をシングルクォーテーションで括ります。
3つ以上ある場合も同様に指定するカラム名を増やせばよいです。
今回は、取り出した2つのデータをさらに変数dfに上書きしてわたします。
実行します。
ディーエフの中身が、2つの列だけになりました。
df = df[:50]
dfこのExcel編では、506個の全部のデータを使うと、わかりにくくなるため、前半50個だけを取り出して使います。
dfから、前半だけを取り出すには、角括弧、コロン、必要な数字です。
dfイコール書いて、df、角括弧、コロン、必要な50という数字を書きます。
50個のデータが取り出せているか見るために、再度dfを書きます。
実行します。
インデックスが49までのデータが取り出せました。
なお、インデックスの最初が1ではなく0です。
したがって、インデックスが49までで、データとしては50個取り出せています。
必要なデータをエクセルファイルでの書き出し
df.to_excel('./ボストンの住宅価格.xlsx')それでは、取り出したデータフレームをエクセル形式で書き出して見ましょう。
dfと書いて、ドット、to_excle丸括弧。
引数には、保存先のパスをシングルクォーテーションで括って与えます。
エクセルファイルなので、最後の拡張子は、xlsxとしましょう。
実行します。
データが書き出されました。
それでは、書き出したデータをエクセルで開いて見ましょう。
エクセルで散布図を作成する
from IPython.display import Image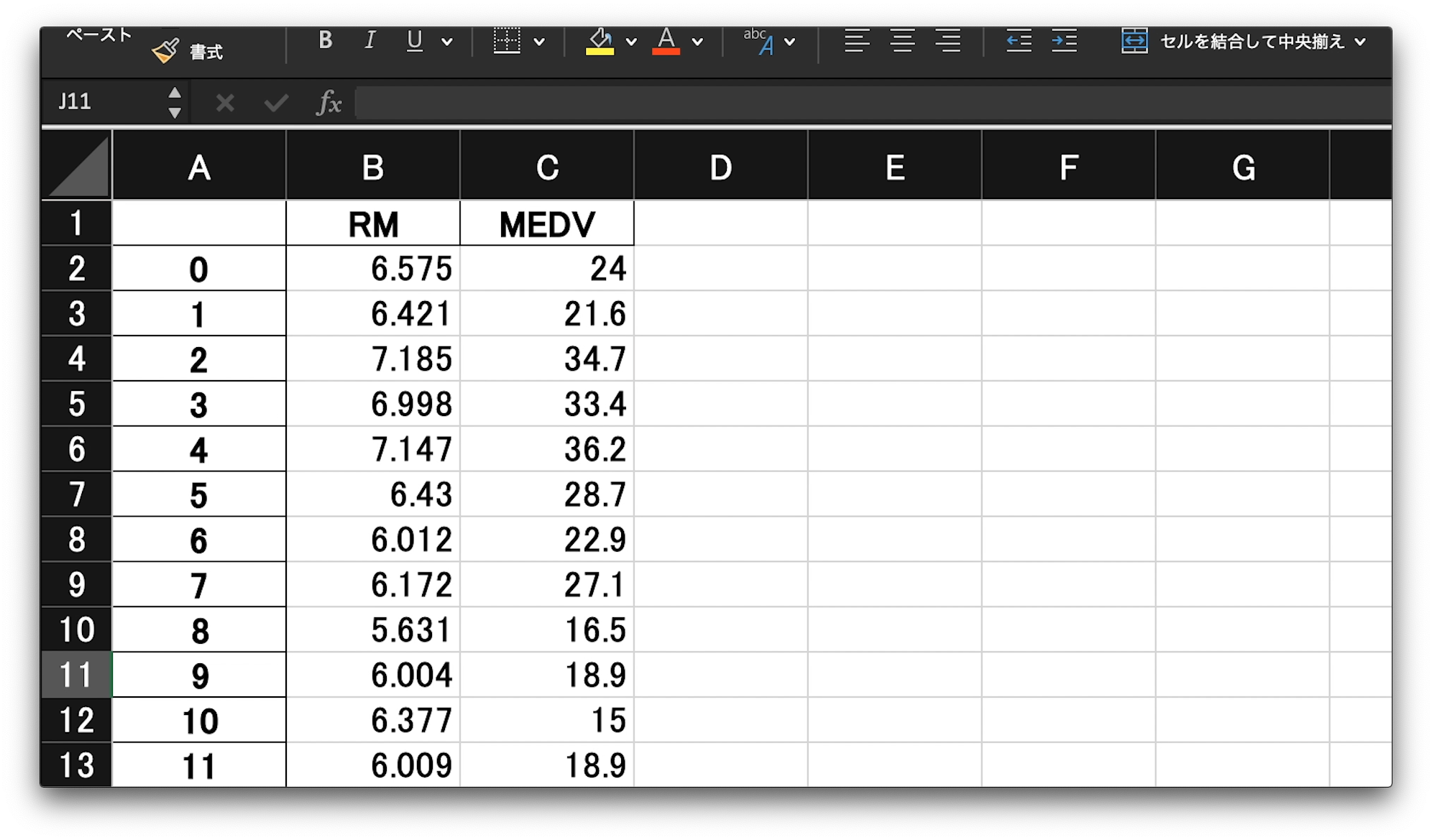
書き出したデータをエクセルで開くと、スライドのようになっていると思います。
左から、インデックスの列、RM、つまり、部屋数の平均の列、最後に、MEDV、つまり、住宅価格の中央値の列となっているはずです。
まずは、このデータを散布図で可視化してみましょう。
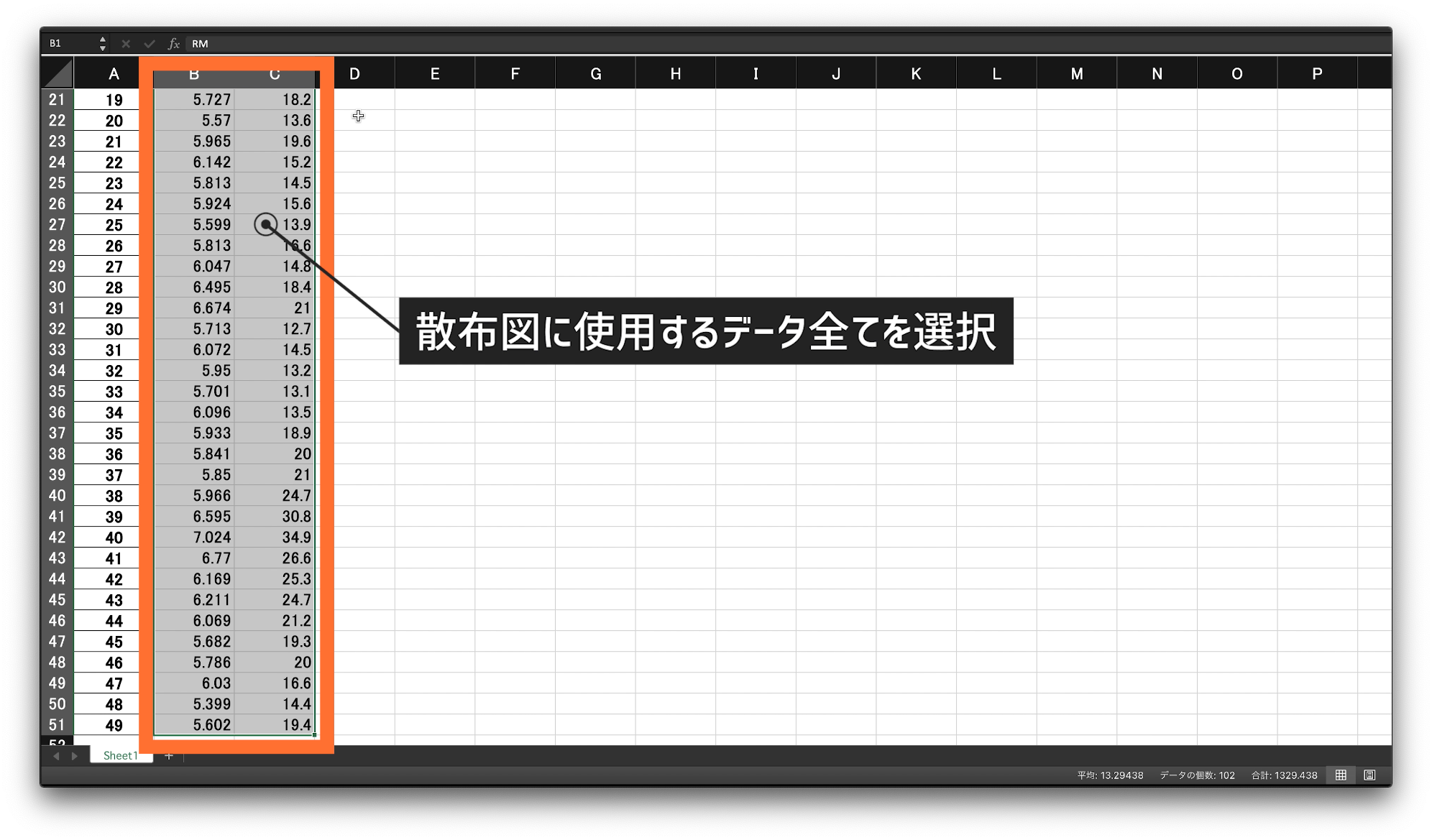
エクセルで散布図を作成する方法です。
まず、スライドのように、散布図のデータと使用するデータを全て選択します。
この状態で、画面、上部、ホームの横の挿入をクリック。
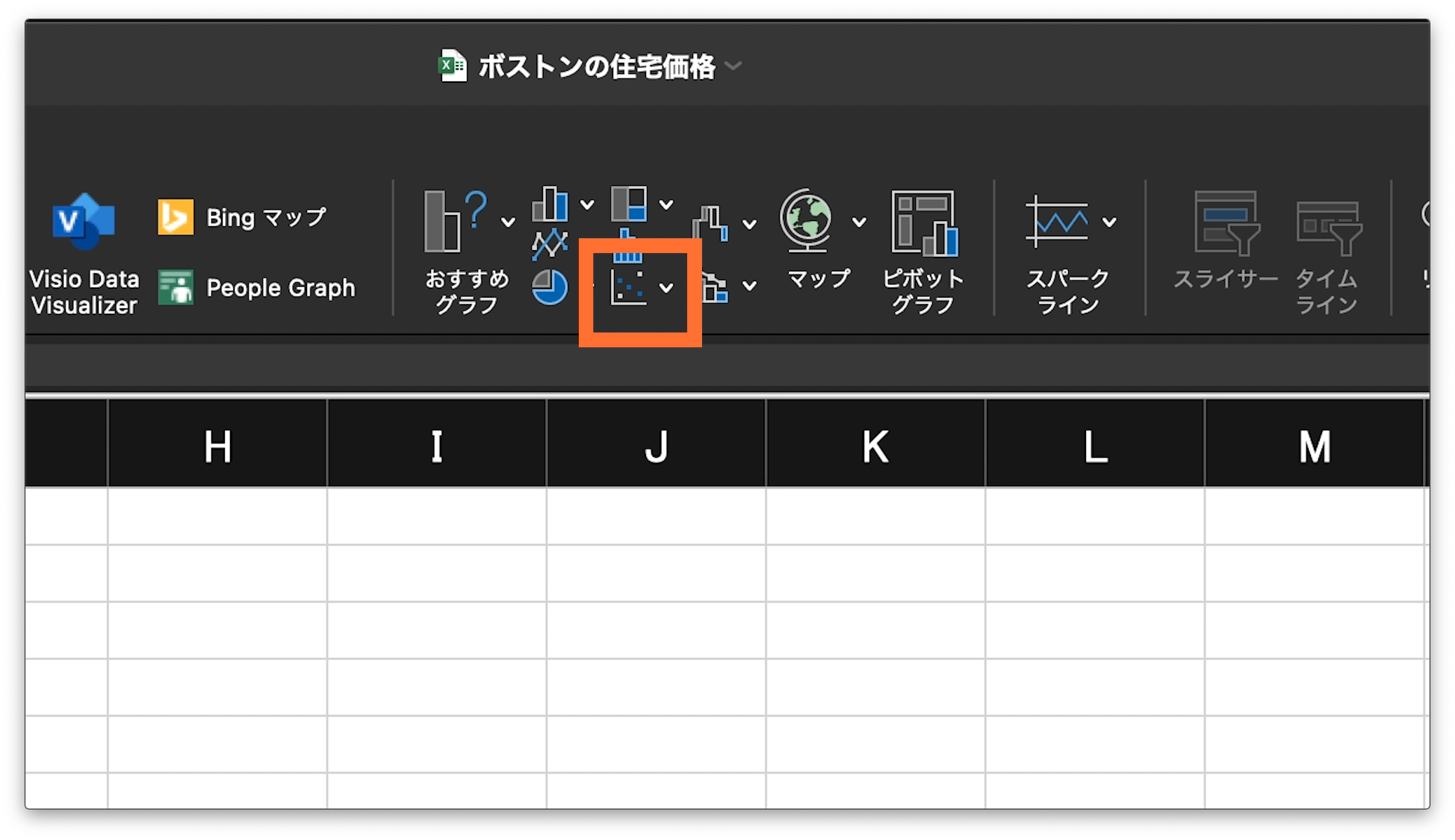
上部のメニューが切り替わります。
このメニューの中央付近、おすすめグラフと表示された部分があるはずです。
そのおすすめグラフの右側に、たくさんのグラフアイコンがあります。
散布図は、そのたくさんのアイコンの一番下、の中央、点々が表示されているアイコンになります。
そこをクリックします。
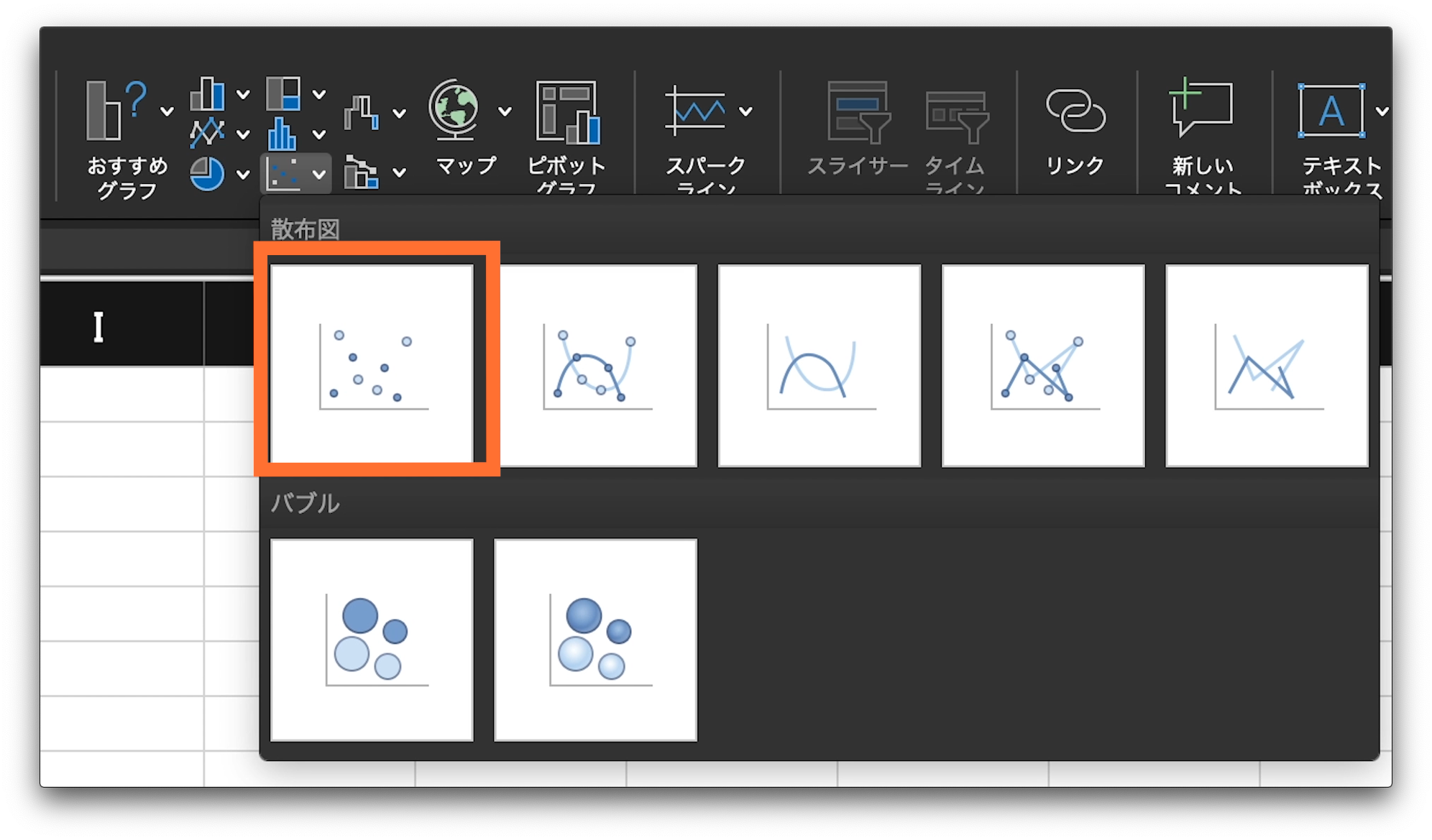
そうすると、いくつかのグラフの候補が表示されます。
それの一番左上、純粋な散布図をクリックします。
そうすると、散布図が出力されます。
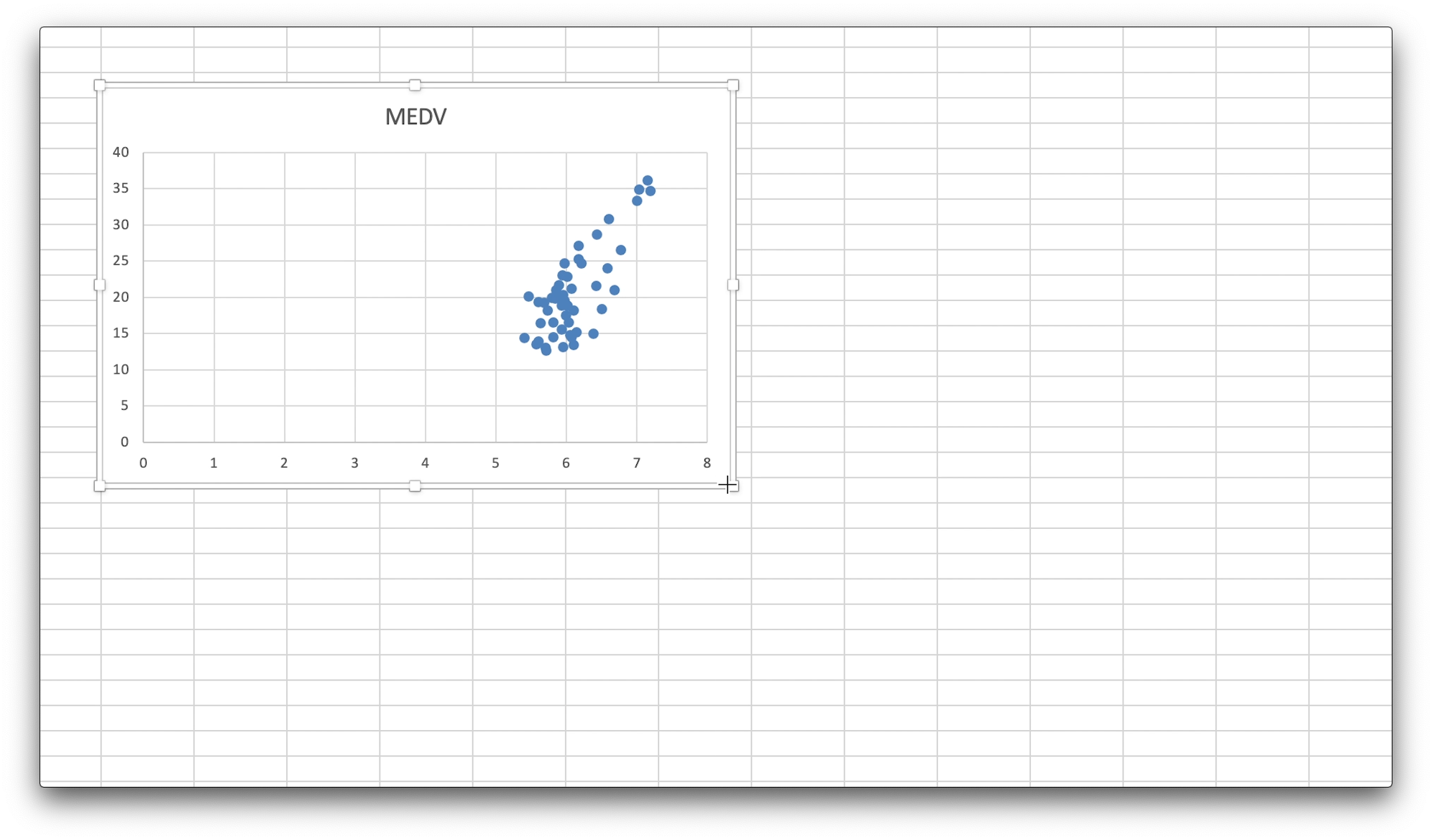
標準で出力される、散布図は少し小さいと思います。
ですので、四隅のグラフエリアをドラック、アンド、ドロップで適宜、見やすい大きさに変更してください。
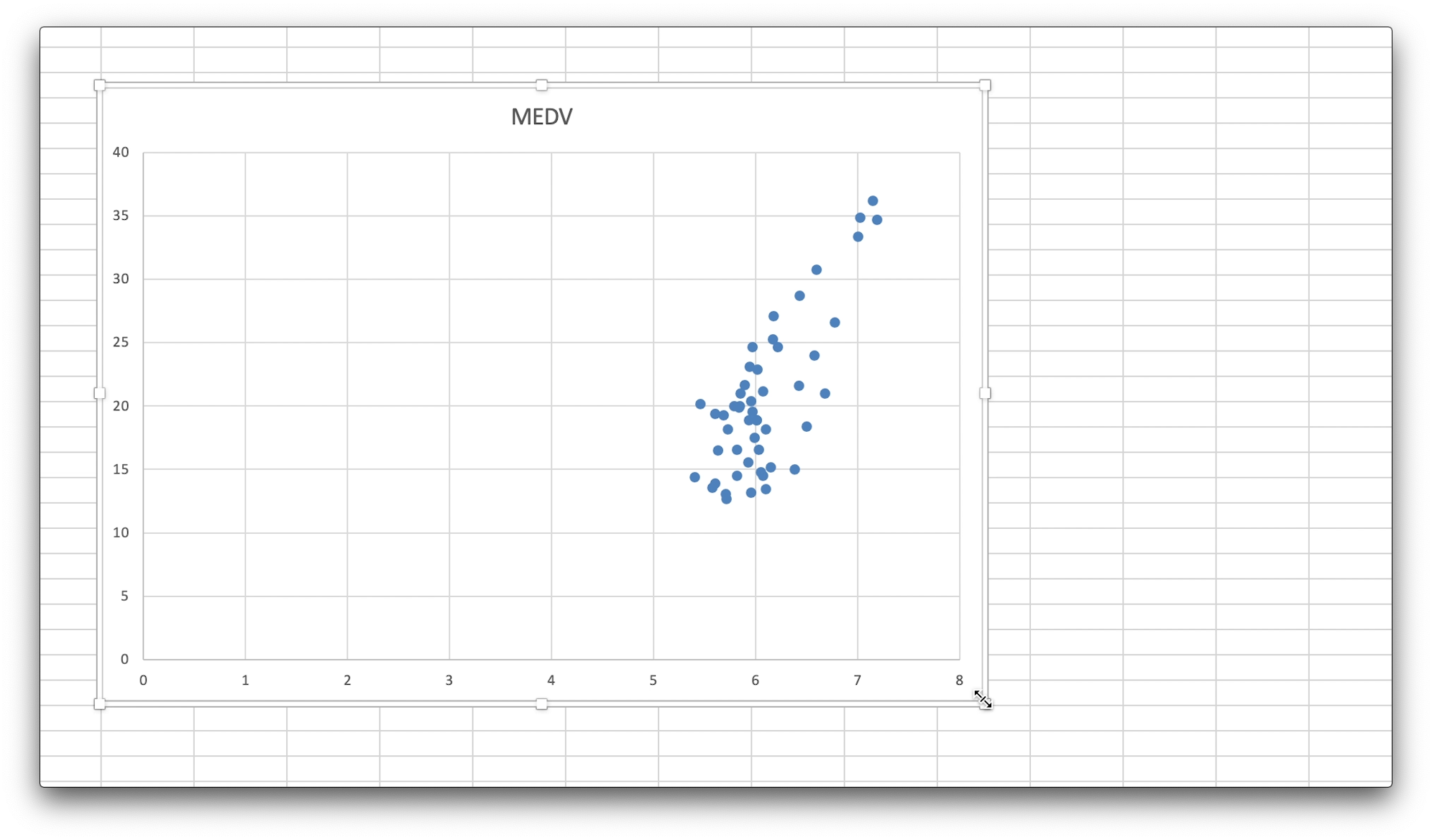
散布図を大きくしました。
なお、散布図は基本的に、選択したデータの左側が横軸、今回ではRM、部屋数の平均の値となります。
ですので、縦軸がMEDV、住宅価格の中央値の値になります。
散布図をみると、部屋数が多ければ多いほど、住宅価格が高くなるような傾向がある気がします。
この気がするは数学的にはどれぐらいなのか、単回帰分析を行い、また、相関・決定係数もみていきましょう。
エクセルで各係数を計算する

さて、ここで、前回動画の復習です。
単回帰の線形回帰分析は、最小二乗法によって、直線を求めることだと説明しました。
直線を求めるとは、中学生のころに習った直線の方程式、y、イコール、a、x、プラス、bの、aとbを求めることです。
機械学習の分野では、係数は、重み、wを使用されることが多いことは前回もご紹介しました。
ですので、ここでは、aをw1、bをw0として式を書いています。
また、前回の「数学を使って理解編」では、最小二乗法によって残差の二乗和を数式で表示しました。
そして、偏微分でできた数式を連立方程式で解くことで、w1とw0を求めることができる、というところまで説明しました。
具体的な計算過程は省略しますが、連立方程式を解くと、この式が得られます。
それでは、この式の通りに計算を行い、w0、w1の値をエクセルで求めていきます。
w0を求めるには、まず、w1を求めなければならないので、w1を求めていきます。
w1を求めるために必要な値を計算していきましょう。
右側に計算で使用する変数などを配置しています。
aveは、英語の平均、アベレージの略称です。
つまり、ave、yなどには、yの値の平均をすぐ下のセルに入れていく予定です。
なお、これらの配置に深い意味はないので、ご自身の見やすいようにしていただけば良いです。
また、セル名もご自身のわかりやすいようにご入力ください。
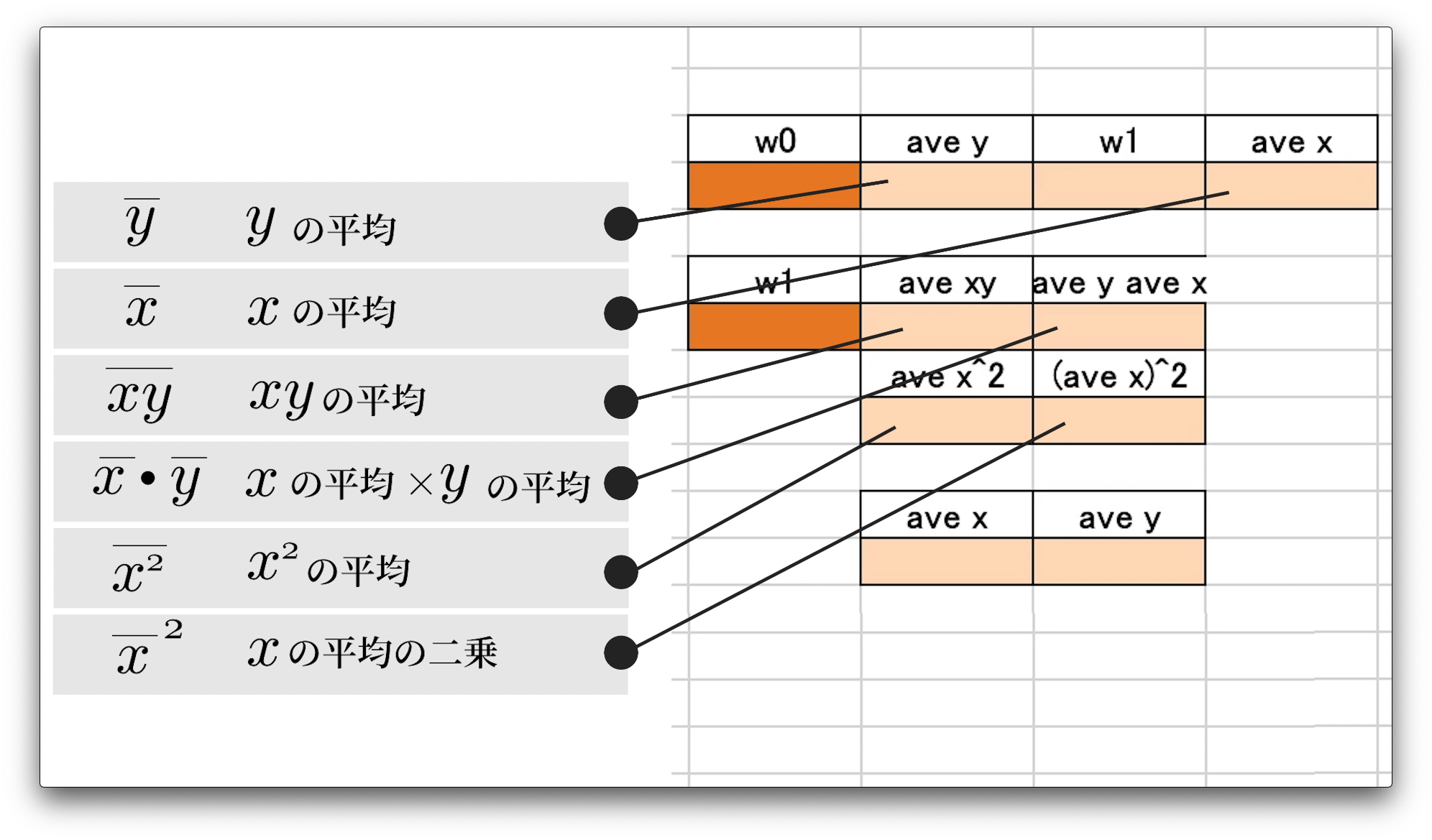
どのセルがなんの値を求めているのかわかりやすくしていきます。
エクセル左の1つ目インデックスを右クリックします。
そうするとスライドのようなメニューが出てくるので、挿入をクリックします。
エクセルの一番上に、空白の行が1行追加されます。
エクセルの追加された、1番上の行の、RMの上のセルに「x」、MEDVの上のセルに「y」を入力します。
今回は、住宅の中央値、MEDVが目的変数なので「y」、部屋数の平均が、説明変数なのでRMを「x」として扱っています。
次に、MEDVのすぐ横のセルに、エックスのハット、2と書きます。
エクセルでは、ハットが乗数計算に使用される記号になります。
ここには、記号の通り、x、つまり、RMの各値を2乗した値を入力していきます。
そのすぐ横のセルに、「x*y」と書きます。
エクセルで、掛け算は、Pyhonと同じく、アスタリスクが計算記号になります。
先ほどと同じく、記号通りの計算、xとy、つまり、RMとMEDVの各値をかけた値を入れていきます。
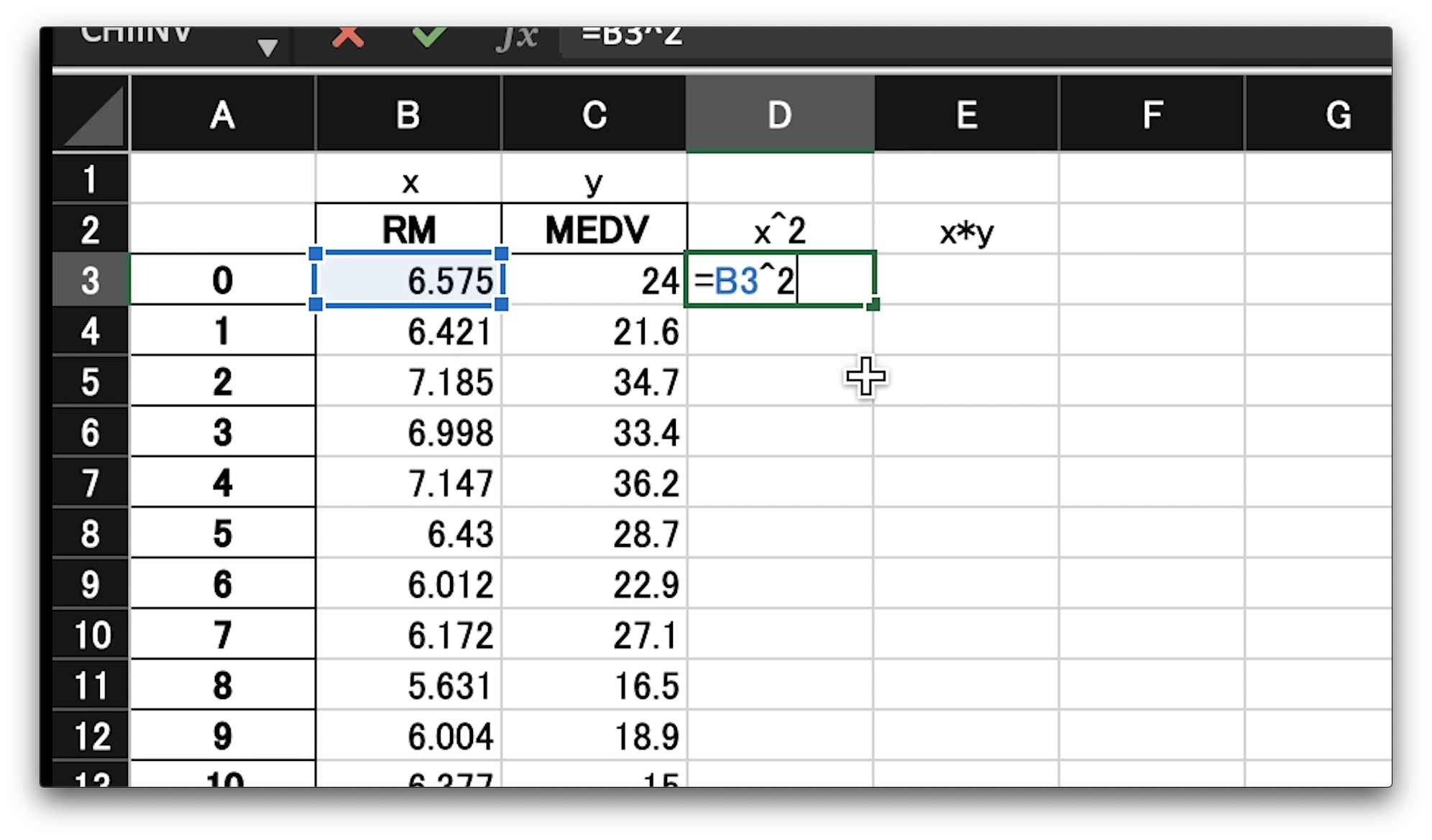
最初に、エックスの2乗の値を入れていきます。
エクセルでは、セルを選択し、半角イコールを入力すると数式モードに切り替わります。
その状態では、マウスで計算に使用したい値が入ったセルを選択できます。
2乗したい値が入った、B3のセルを選択します。
選択すると、入力セルには、その選択したセル番号が自動で入力されます。
また、選択中のセルは視覚的にわかるようにマーカーが表示されます。
この、選択した、エックスの値を2乗したいので、ハット、2と書きエンターです。
アールエムの最初の6.575が2乗された、43.23…という数字が表示されました。
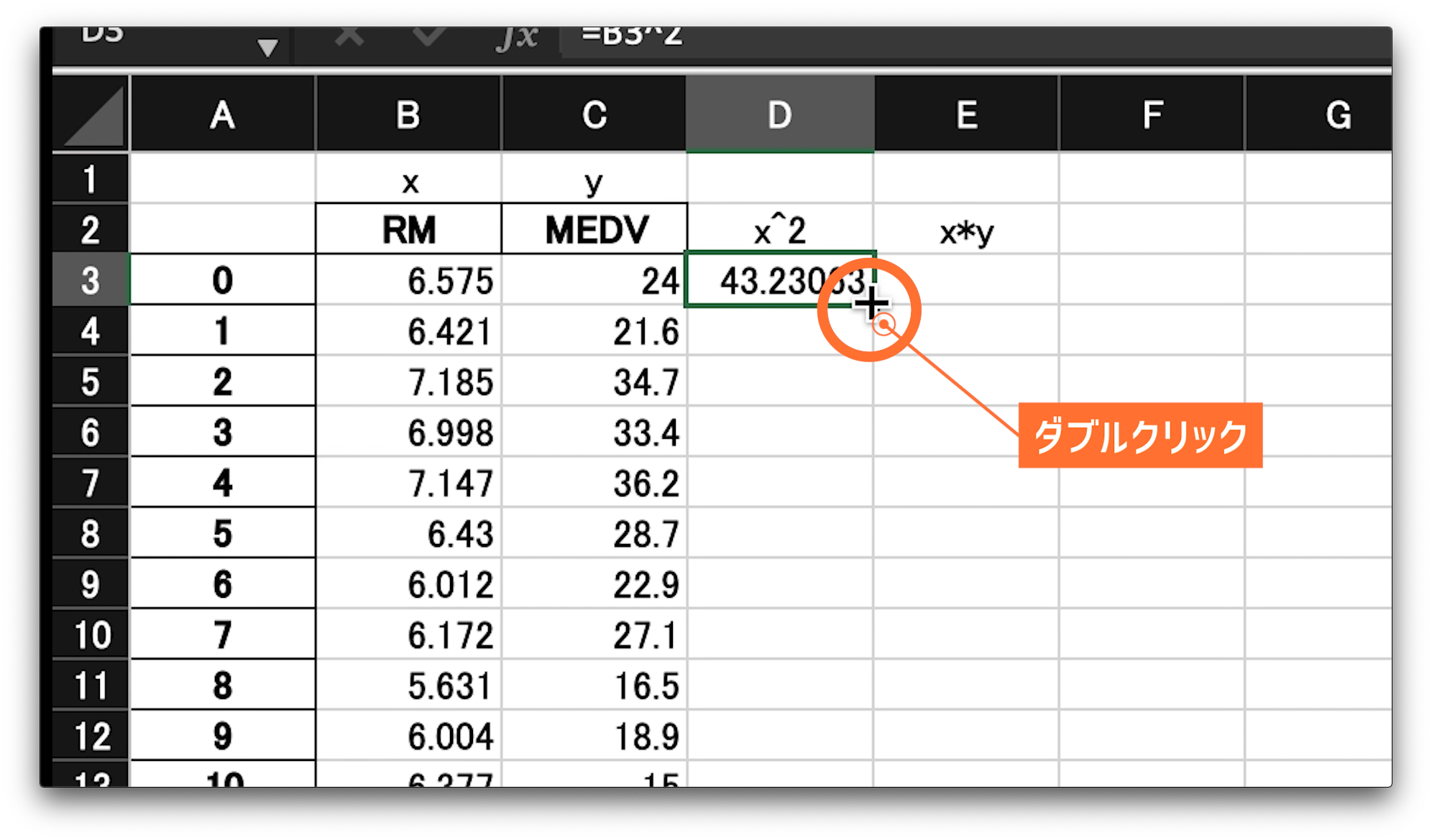
ここから、全てのセルに同じ操作を。。。
とは言いません
エクセルでは、同じ計算を一瞬で行ってくれる機能があります。
先程の、ビー3を2乗した値が入っている、ディー3のセルを選択してください。
そうすると、の右下の角に緑の小さい四角が表示されるので、それをダブルクリックしてください。
RMの全ての値に対して、2乗された値が入力されました。
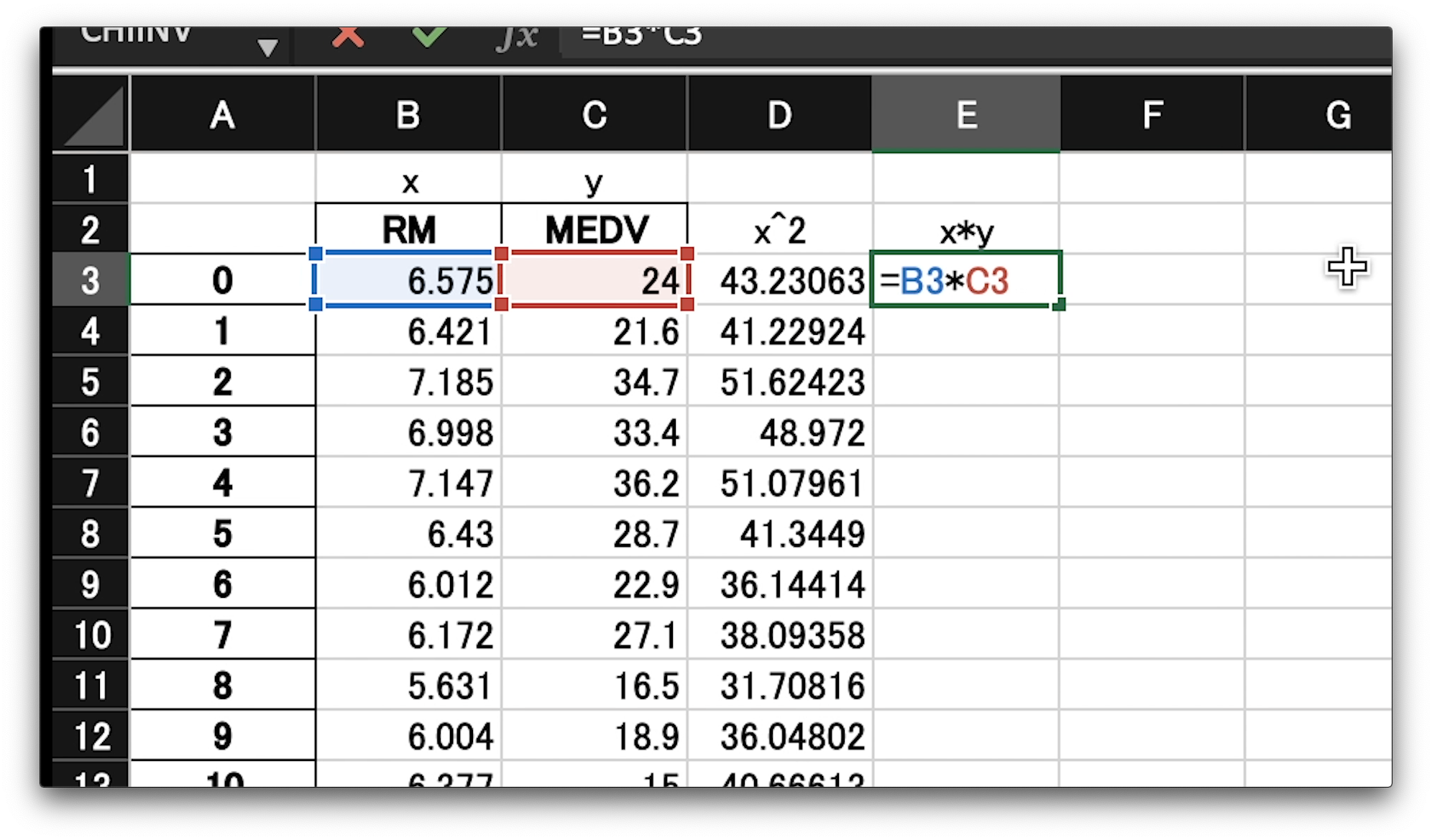
「x」と「y」をかけた値も同じ要領で計算していきましょう。
今度はE3のセルに、イコール、B3とC3のセルを掛け合わせる数式を書きます。
掛け算記号は、アスタリスクです。
エンターを押して、右下、緑、四角をダブルクリック、全てのセルに計算を実行します。

それでは、セルに値を入力していきます。
まずは、セルH3のyの平均から計算していきます。
H3にイコール、averageと入力すると、エクセル関数の平均を求めるaverage関数を使えます。
Pythonと同じく、かっこの中に引数を与えることで計算できます。
average関数はそのまま、与えられた全ての値の平均を出力してくれます。
「y」、つまり、MEDVの平均を求めたいので、C3のセルを選択します。
そのまま、ドラッグ・アンド・ドロップで、「y」の最終行までを選択しましょう。
最後に丸括弧閉じを入力し、エンター。
「y」の平均値が計算されています。
先程、「x」の各値の2乗と、「x」と「y」をかけた値を全て出力したのは、それらの値の平均を求めやすくするためでした。
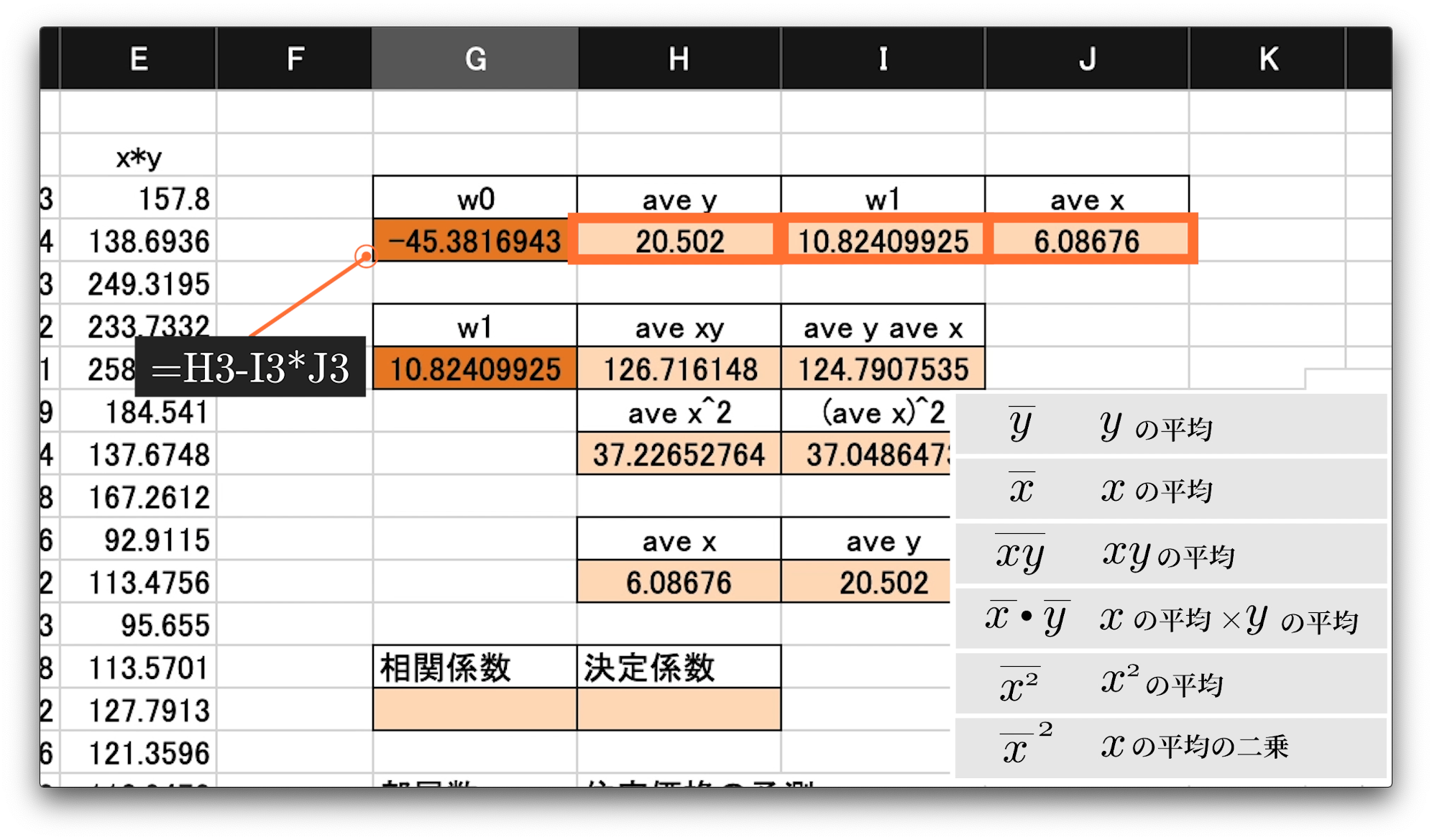
それでは、ここまでの知識を使って、残りのセルに必要な数式を入力し、値を計算してみてください。
なお、割り算記号はスラッシュです。
まだ、エクセル操作が慣れていなくて数式がわからない方は、次を参考に数式を入力してみてください。
各セルへの入力値は以下です。
G3 = H3-I3J3
H3 = AVERAGE(C3:C52)
I3 = G6
J3 = AVERAGE(B3:B52)
G6 = (H6-I6)/(H8-I8)
H6 = AVERAGE(E3:E52)
I6 = I11H11
H8 = AVERAGE(D3:D52)
I8 = H11^2
H11 = J3
I11 = H3
計算式については、先ほどご紹介した通りですが、わからない方はキノコードのウェブサイトにExcelを保存しております。
そこでも計算式を確認してみてください。
さて、これでw0とw1の値が求められました。
これで、回帰直線を求めることができました。
相関係数と決定係数の計算
続いて、相関係数と決定係数をエクセル関数で求めてみましょう。
相関係数はCORREL関数、決定係数はRSQ関数を使用します。
どちらも、「x」の全てのデータを、1つ目の引数。
「y」の全てのデータを2つ目の引数として渡すことで、それぞれの係数を求めることができます。
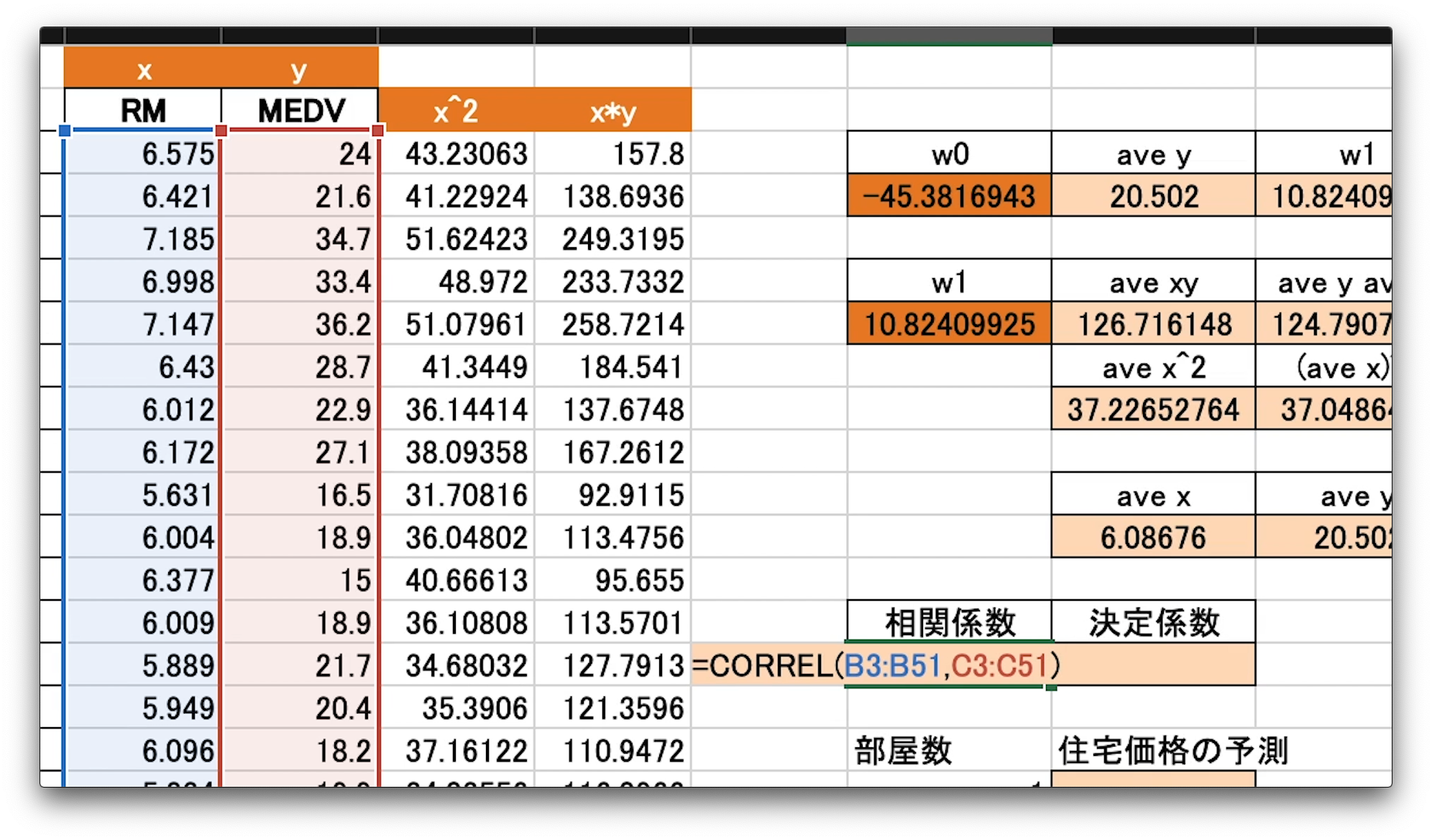
相関係数を求める、CORREL関数を例にみてみましょう。
相関係数を入れたい、G15セルを選択し、イコールを入力します。
CORRELと書き、括弧、1つ目の引数として、「x」の全てのデータを選択します。
選択できたら、カンマをかき、同じく「y」の全てのデータを選択します。
括弧を閉じて、エンターです。
決定係数のRSQ関数も同様に計算してみましょう。
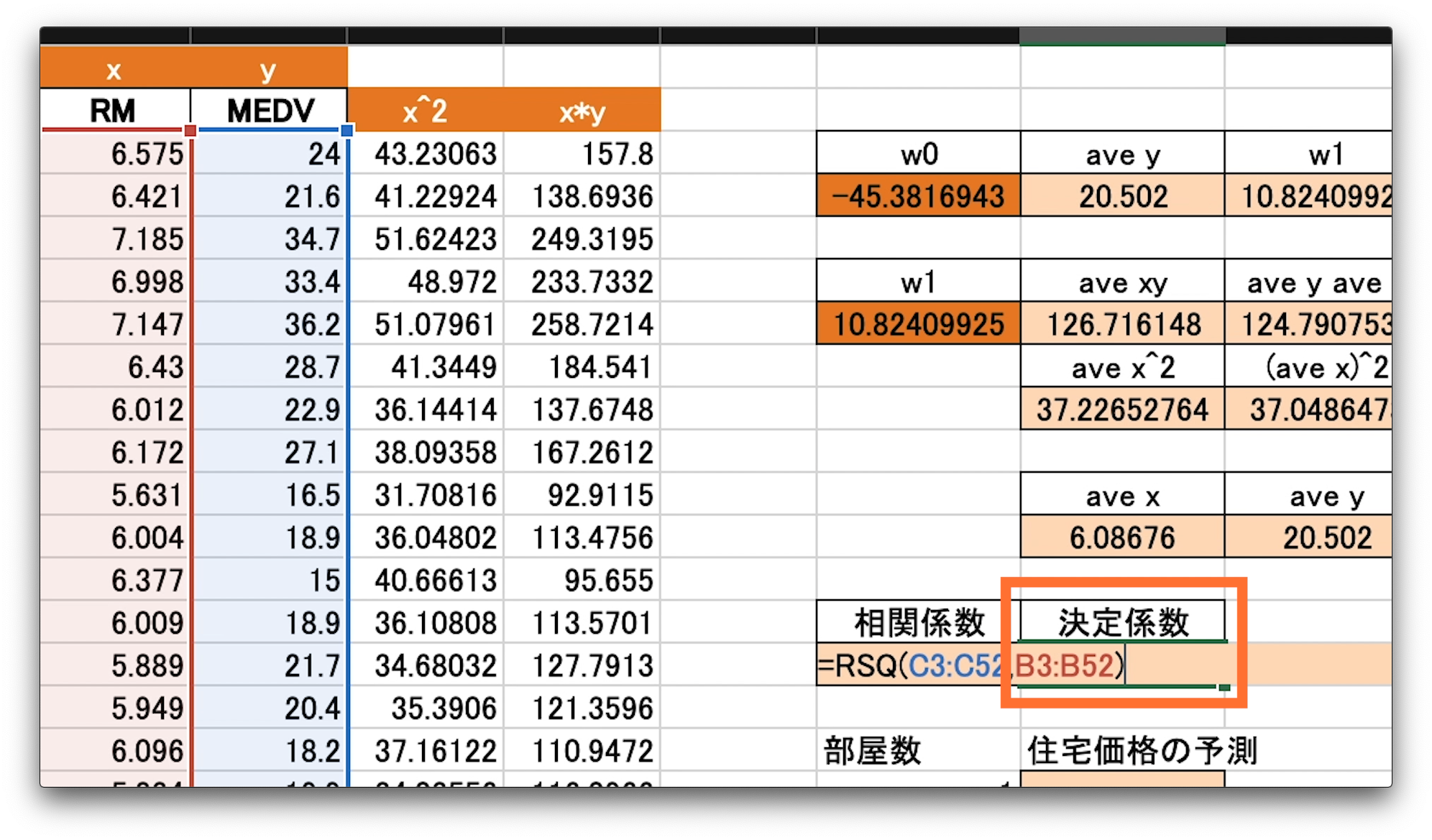
これで全ての係数をエクセルで計算することができました。
相関係数が0.77弱とそれなりに正の相関があるようですね。
グラフによる回帰分析・決定係数の出力
ここまで、エクセル関数を使用しながら、一つ一つ丁寧に計算することで各係数を求めてきました。
実は、エクセルの散布図には、回帰直線を一瞬で表示し、なおかつ各係数も一瞬で出力する方法があります。
この動画の現時点までは、数学的な理解を深めるために、細かく計算してきました。
遠回りはしましたが、きっと理解に役立つはずです。
どうやって計算しているのか上司や同僚につっこまれたとしても回答できるはずです。
ただ、スピードが求められる場合では、今から紹介する方法で、回帰分析を行うと良いでしょう。
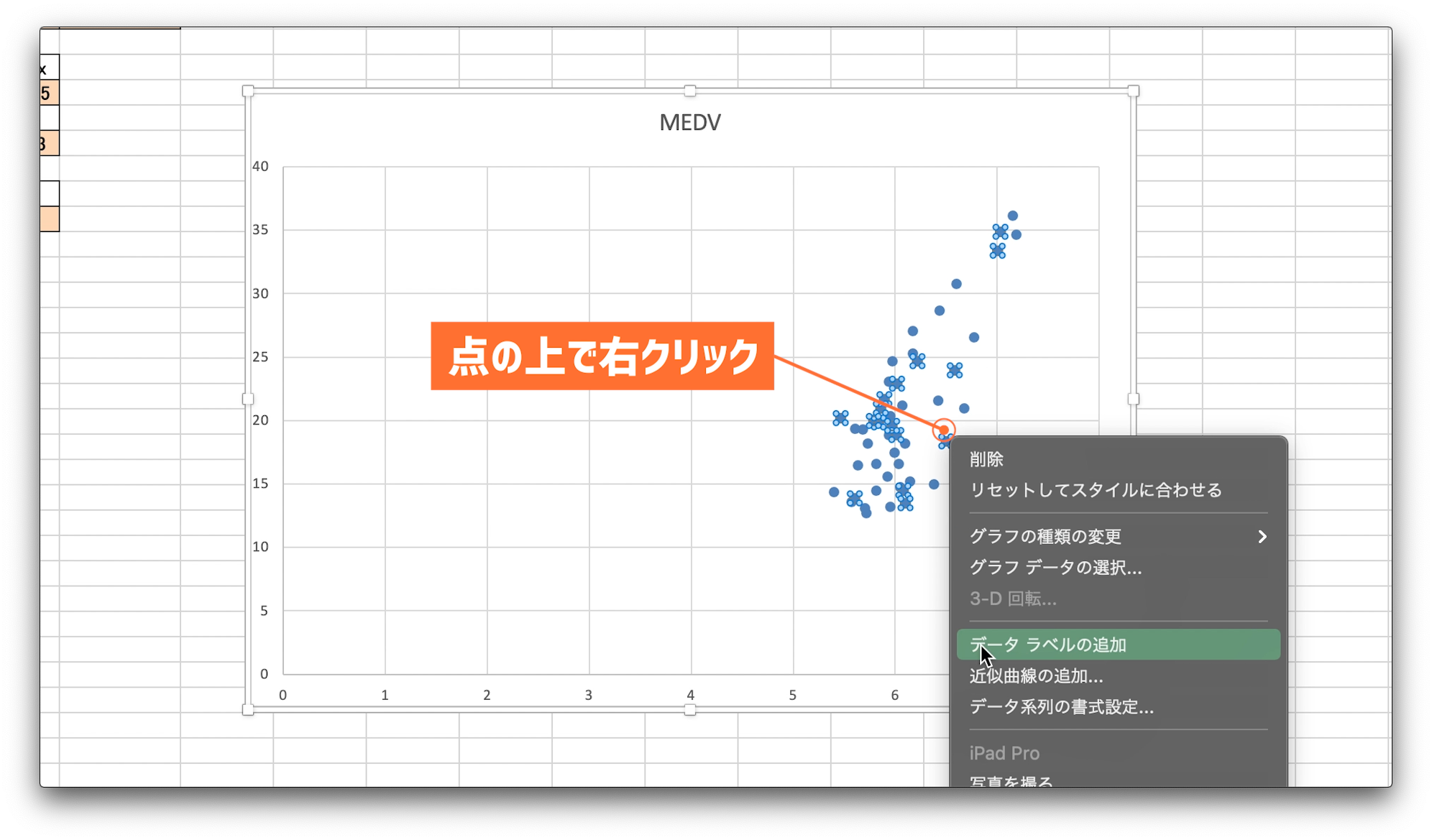
先程作成した散布図を表示します。
次に、プロットされているデータの点の上で右クリック。
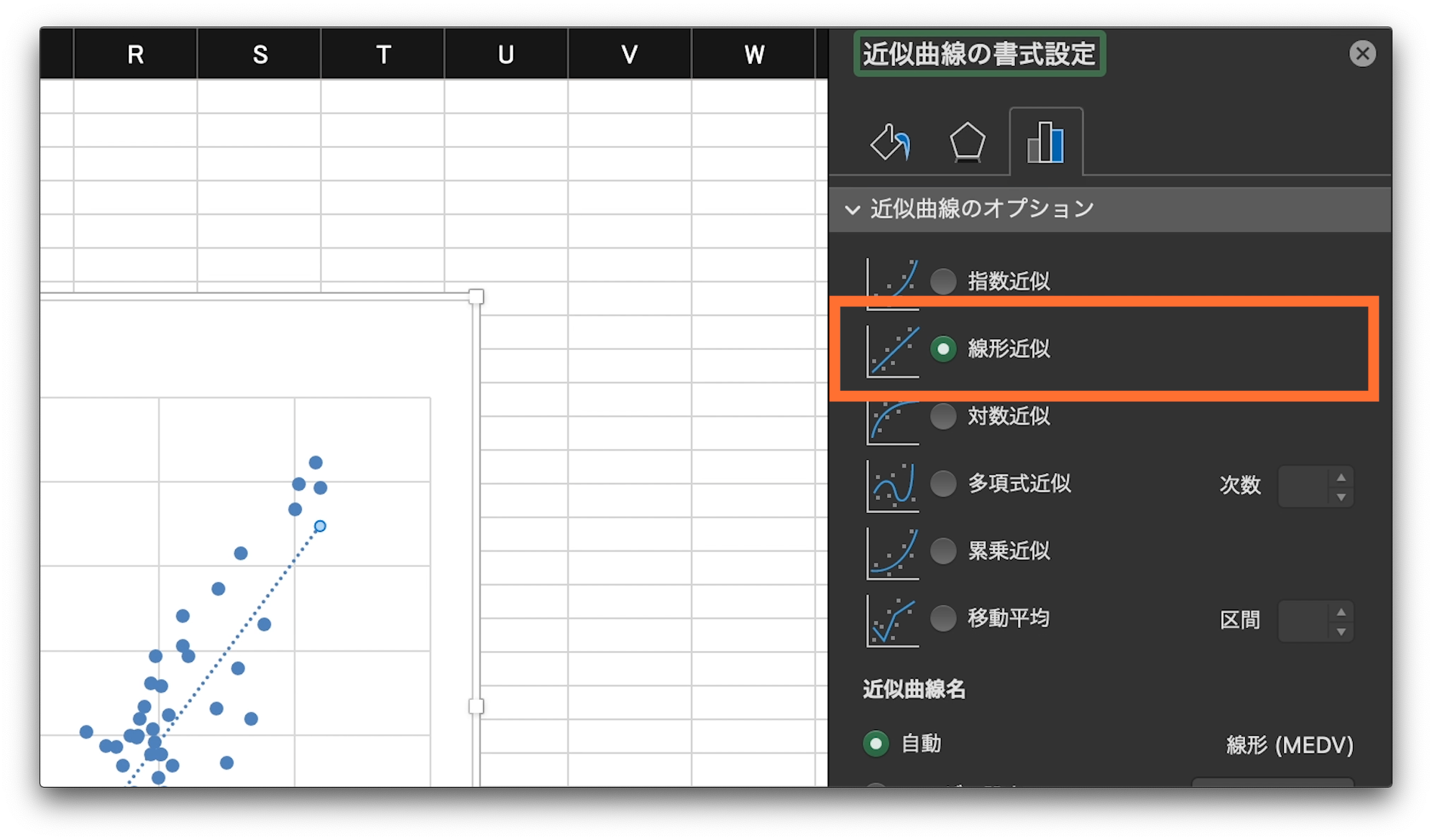
そうすると、近似曲線の追加という項目があるのでクリック。
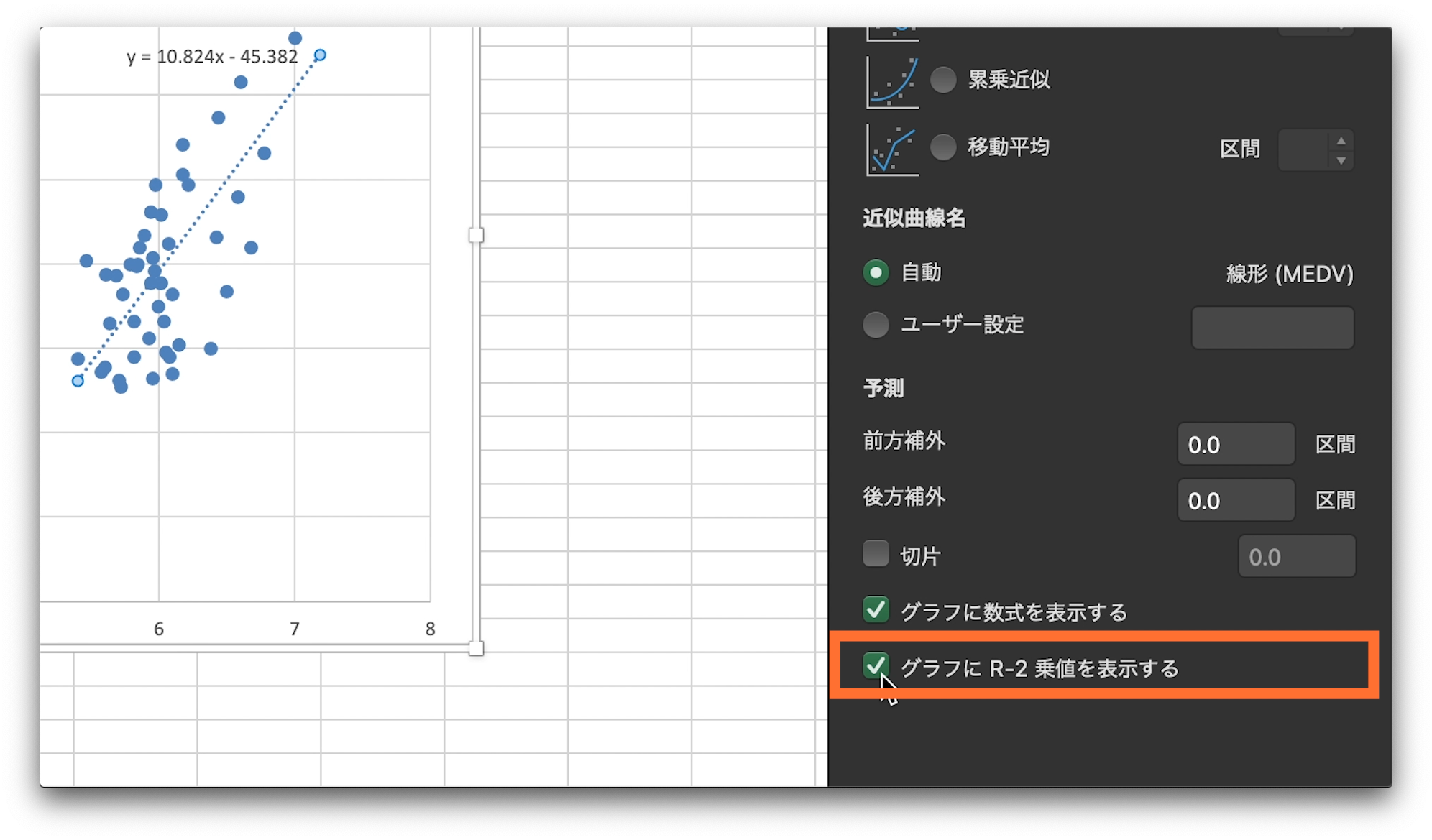
近似曲線の書式設定が表示されるので、線形近似のボタンにチェック。
これで、回帰直線が表示されます。
また、近似曲線の書式設定の下の項目、グラフに数式を表示するにチェック。
グラフにR-2乗値を表示するにチェック
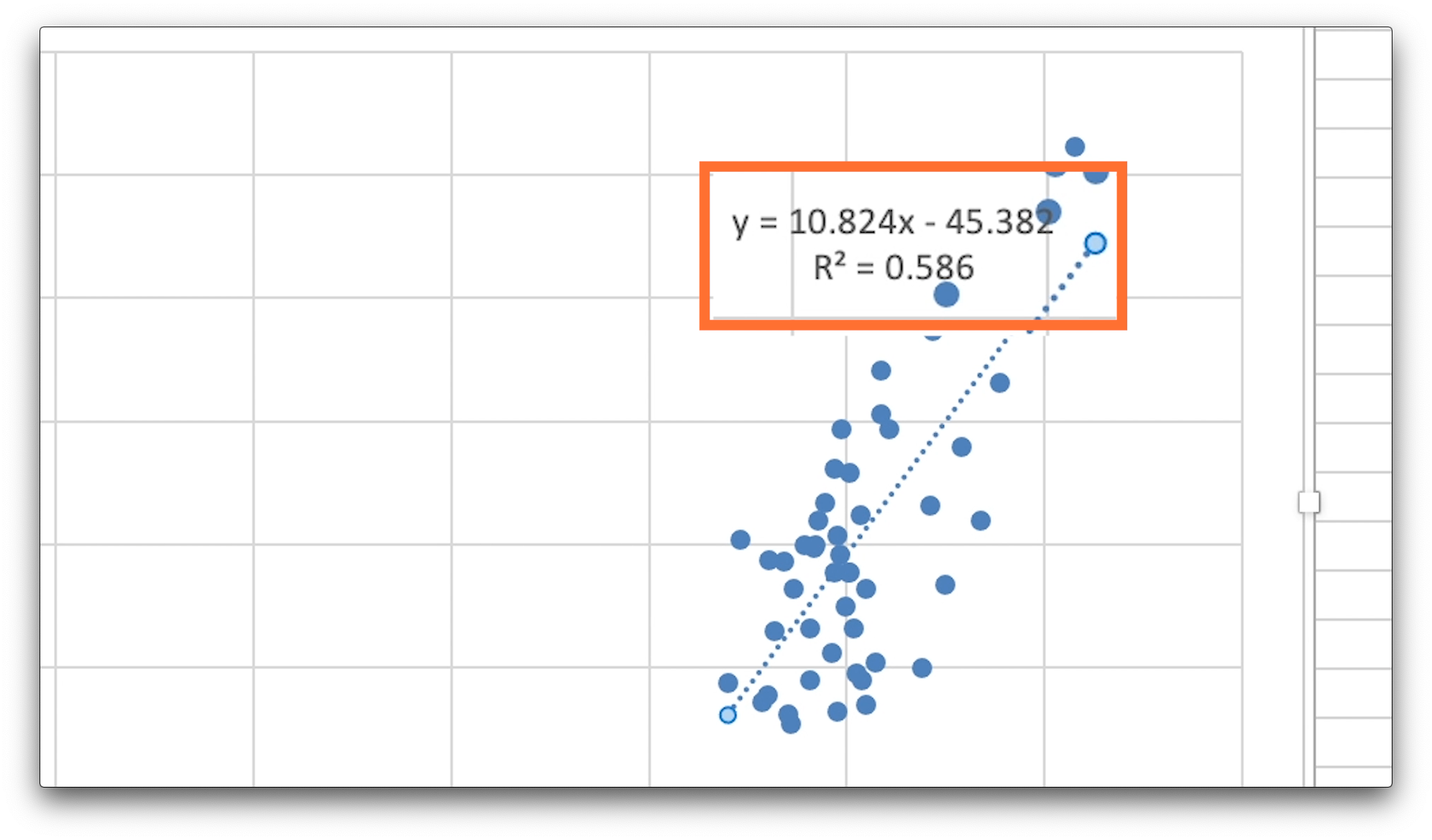
そうすると、回帰直線の数式と決定係数が表示されます。
数式の右辺、xの係数が、w1、数字のみの値がw0の値と同じになっているはずです。
四捨五入を考えれば、両方の係数とも同じです。
しっかりと、w0、w1が求められていましたね。
また、大文字アール、2乗の値が決定係数です。
こちらも、先程求めた決定係数と同じ値なので、しっかりと計算できていたようです。
回帰直線による住宅価格の予測方法
を予測してみます。
部屋数となる、数字を1から10セルに入力します。
住宅価格の予測のセルに、求めたw0とw1を使用して、住宅価格の予測式を入力します。
イコール、切片となる、w0、足すことの、w1かける部屋数です。
計算式についているドルマークは、計算をセルを変化させて行っても、指定のセルは変更しないようにするというエクセル関数の書き方です。
部屋数がエックスで、w0とw1の値は変わりません。
そこで、w0とw1の値に該当するセル番号にドルマークをつけています。
これを部屋数が1から10の間でどうなるかをみて見ましょう。

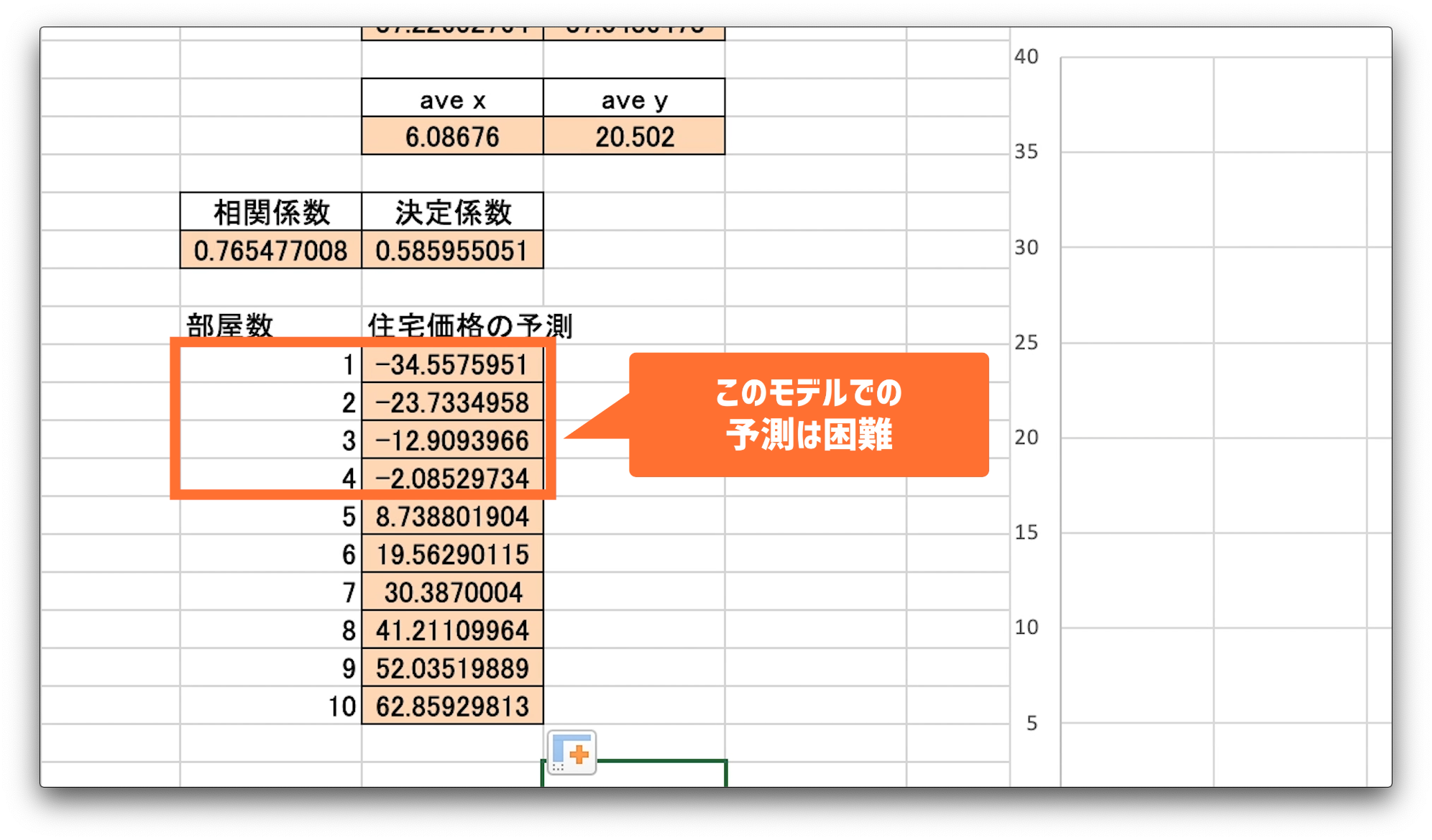
1から4部屋は、住宅価格がマイナスになっています。
住宅の価格がマイナスになるのはありえません。
ですので、1から4部屋までは、このモデルで価格を予測するのは困難なようです。
しかし、部屋数が増えてくればそれなりの住宅価格になっているので、予測モデルとして使えるかもしれません。
このようにして、線形回帰モデルは目的変数の値を予測することができます。
また、相関係数や決定係数を見ることで、2変数間の関係性などについても考察することができます。
一見、地味に見えるかもしれませんが、単回帰分析は、データ分析の基礎的内容です。
これを機会にマスターして仕事にどんどんいかしていきましょう。
エンディング
単回帰分析、第3回、「エクセルで学ぶ人工知能編」はいかがだったでしょうか。
ここまで、見てくださりありがとうございました。
次回は、いよいよパイソンでの実装になります。
それでは、次のレッスンでお会いしましょう。