【10分でロジスティック回帰の概要がわかる】AI講座 第12回｜Pythonではじめる人工知能入門講座

こんにちは。
キノコードです。
AI講座の単回帰分析、重回帰分析の動画はすでにご覧いただけましたか？
単回帰分析、重回帰分析は機械学習の基礎的な内容です。
まだご覧になっていない方はぜひチェックしてみてください。
そして、今回解説するのはロジスティック回帰分析です。

このロジスティック回帰分析を含めたAI講座では、1つの分析手法を4つのパートに分けて解説していきます。
今回はロジスティック回帰分析の「ゼロからわかる理論編」です。
この「ゼロからわかる理論編」では、数学や統計学の知識は置いといて、ロジスティック回帰分析がどのような分析手法なのか、ということについて解説していきます。
より詳しく知りたい方は、次の数式を使って理解編で解説していますので、合わせてご覧ください。

なお、キノコードでは人工知能のレッスンのほかに、たくさんのプログラミングに関するレッスンを配信しています。
チャンネル登録がまだの方は、チャンネルがどこに行ったか分からなくならないように、是非チャンネル登録をお願いします。
それではレッスンスタートです。

ロジスティック回帰分析とは

まず、ロジスティック回帰分析とはどのような分析手法でしょうか？
ロジスティック回帰分析とは、手元のデータから目的のデータを分類する手法です。
以前紹介した単回帰分析は、大きさを比較できる量的データの予測に使用されると説明しました。
ロジスティック回帰分析は、大きさを比較できない質的データの予測に使用されます。
例えば、前日までの株価のデータから、翌日の株価が上がる下がるかを予測する。
喫煙、飲酒、運動などの生活習慣からその人が病気になるかならないかを予測する、といった場合に活用できます。
ロジスティック回帰分析は「回帰」という名前が付いていますが、最終的に目的のデータを分類する手法だということを忘れないでください。

ロジスティック回帰分析の手法

それでは、ロジスティック回帰分析の手法について図を使ってわかりやすく説明していきます。
例えば、このような130本のワインのデータがあったとしましょう。
それぞれのデータにはワインの色味の強さと、そのワインの種類が記載されています。

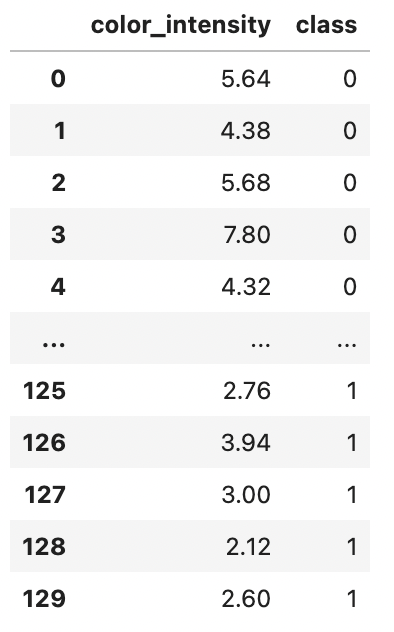
全部のデータを集計して、x軸をワインの色味の強さ、y軸をそのワインの種類がクラス0かクラス1かとしてプロットすると、このようなグラフになリます。

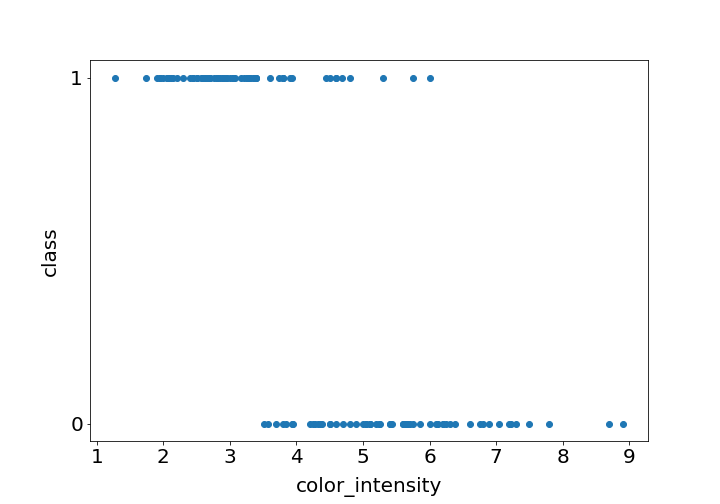
ここから新たに違うワインの色味の強さがわかったとき、ロジスティック回帰分析を使うとそのワインの種類がクラス0かクラス1かを予測できます。
ではどのように予測するのでしょうか？
ロジスティック回帰分析では目的のデータの確率を考えます。
ここで、確率にはいろいろな表し方があります。
例えば、日常生活でよく使われる勝率80%や降水確率40%など、全体を100とする百分率で表す方法があります。
他にも、野球の打率など、全体を10とする歩合で表す方法もあります。
しかし、数学や機械学習の分野では、全体を1として確率を表します。
従って、確率は必ず0から1の間におさまります。
そこで先ほどのデータを、ワインの種類がクラス1の場合を1、クラス0の場合を0、y軸をワインがクラス1の確率として表してみましょう。

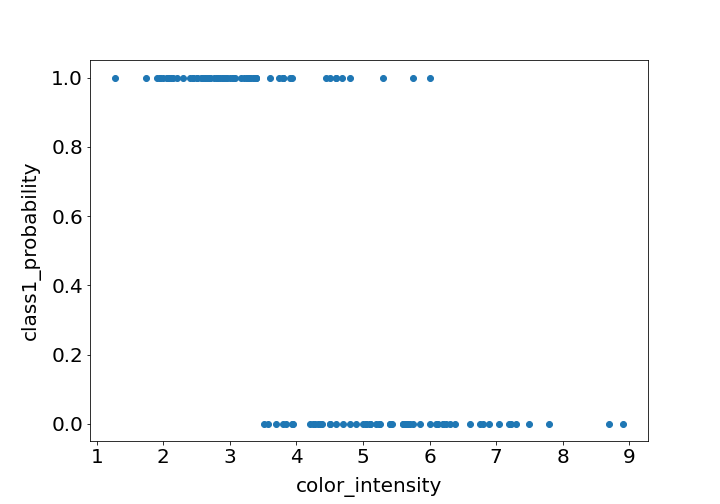
ワインの種類がクラス1ならクラス1の確率が1、ワインの種類がクラス0ならクラス1の確率が0ということになります。
そして、クラス1の確率が0.5以上であればクラス1、クラス1の確率が0.5未満であればクラス0、と分類できそうです。
あとは入力$x$に対して0から1の間の数値を出力するような関数があれば、ワインの種類がクラス1である確率を求められるので、そのワインの種類がクラス1かクラス0か分類できますね。
そこで、このようなロジスティック関数と呼ばれる関数を使います。

$$
p = \frac{1}{1 + e^{-(w{0} + w{1}x)}}
$$

ロジスティック関数の導出などは次の「数式を使って理解編」で詳しく説明しますので、ここではこのような関数を使うんだということだけ覚えていただけると幸いです。
この式を使って$x$に値を代入すると、$p$は0から1の間の値になります。
例として、$w{0}$と$w{1}$に値を代入してロジスティック関数のグラフを描くとこのようになります。

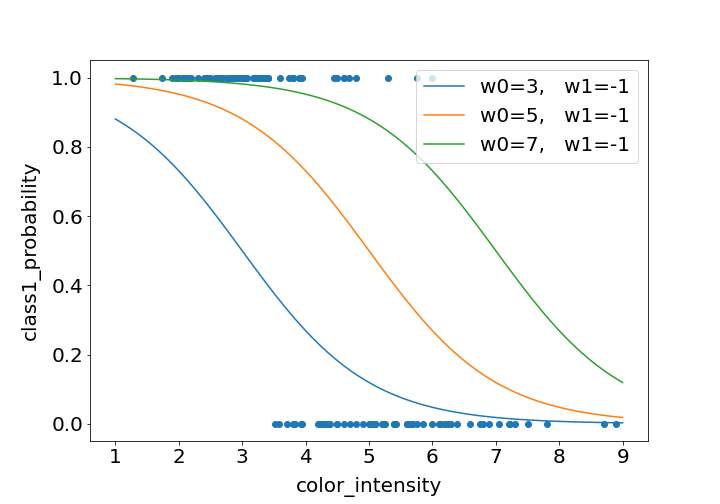
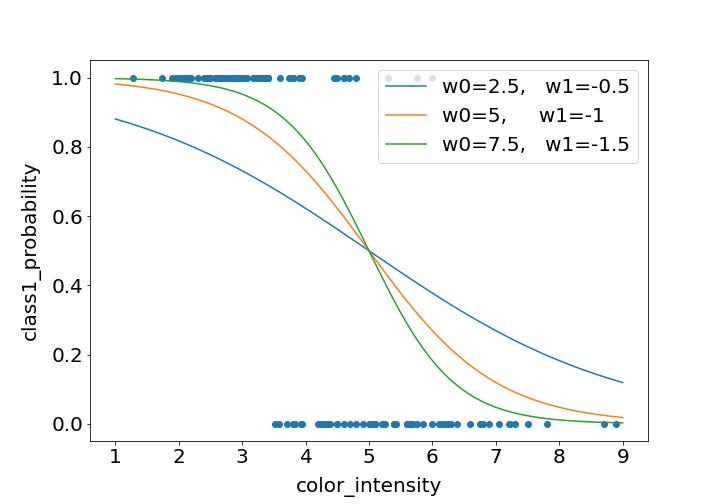
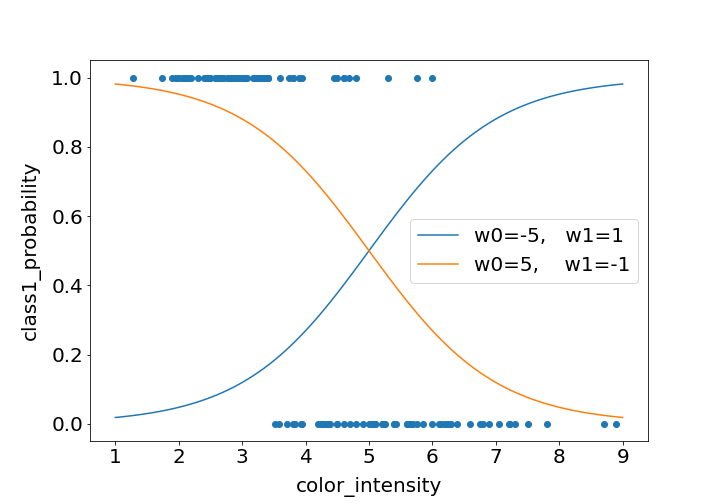
また、y軸の値が減少していく関数だけではなく、増加していく関数にもできます。

あとはできるだけ今あるデータに適合するように、パラメーター$w{0}$と$w{1}$の最適値を求めます。
以前解説した単回帰分析では、最小二乗法という手法を用いてパラメーター$w{0}$と$w{1}$の最適値を求めました。
ロジスティック回帰分析では、このパラメーターの最適値を求めるのに最尤推定法という手法を使うことが多いです。

ここまでの内容はしっかりと理解していただけたでしょうか？
忘れずに復習をするためにも、チャンネル登録を是非お願いします。

最尤推定法

次に、最尤推定法について説明します。
最尤推定法は、得られた結果から一番理にかなった条件を推定する方法のことです。
少しわかりづらいので具体例を出します。
例えば、表が出る確率が2分の1の普通のコインを1000回投げたとしましょう。
その場合、表と裏が出る回数はそれぞれ何回ずつになるでしょうか？
表が500回、裏が500回出る、と考えると思います。
これはコインの表が出る確率が2分の1だと分かっているからですね。
しかし、実際の問題ではこのようにあらかじめ前提条件がわかっていることは少ないです。
そこで、今度は表が出る確率が$p$のゆがんだコインを1000回投げたとしましょう。
そして、表が500回、裏が500回出たとします。
その場合、ゆがんだコインの表が出る確率$p$はいくつになるでしょうか？
1000回コインを投げて500回表が出たので、表が出る確率$p$は2分の1と考えるのが一番理にかなってますよね。
このように、得られた結果から一番理にかなった条件を推定するのが最尤推定法です。
話をまとめます。
一般的な確率の問題は、あらかじめコインの表が出る確率$p$がわかっていて、そこから結果を予測します。
一方、最尤推定法はその順番が逆です。
コインを投げた回数と表が出た回数がわかっていて、そこからコインの表が出る確率$p$を推定します。
つまり最尤推定法を使うと、持っているデータからそのデータを引き起こすパラメーターを推定できます。

これを今回の問題に適用してみましょう。
今、手元には130本のワインのデータがあり、ワインの色味の強さと、そのワインの種類がクラス0かクラス1かがわかっています。
このデータを先ほどのようにプロットします。

最尤推定法は、持っているデータからそのデータを引き起こすパラメーターを推定する手法です。
今回の場合で考えると、できるだけこのプロットの近くを通るような関数の形、すなわち関数のパラメーターを推定するのが最尤推定法です。

パラメーターの推定

それでは、どのようにパラメーターを推定するのでしょうか？
最小二乗法では、残差の二乗和という関数を最小化するようにパラメーターを求めましたね。
詳しい説明は次の「数式を使って理解編」で説明しますが、今回の最尤推定法では、交差エントロピー誤差という関数を最小化するようにパラメーターを求めます。
具体的には、まずパラメーターに適当な値を代入して交差エントロピー誤差を求めます。
そして、交差エントロピー誤差が最小になるようにパラメーターを逐一更新し、パラメーターの最適値を求めます。
このようにして求められたパラメーターの最適値から、関数の式を決定します。
関数の式がわかれば、ワインの色味の強さからそのワインの種類がクラス1である確率が求められます。
そして、クラス1の確率が0.5以上であればクラス1、クラス1の確率が0.5未満であればクラス0、と分類します。
これがロジスティック回帰分析の分析手法です。

　まとめ

最後に、今回説明したロジスティック回帰分析をおさらいしましょう。
ロジスティック回帰分析では、まず目的変数を0と1で表し、目的変数の確率を考えます。
次に、その確率をロジスティック関数を使って表します。
そして、その確率ができるだけ実際の目的変数と適合するように、ロジスティック関数の形を決めるパラメーターを最尤推定法で求めます。
パラメーターが決まれば、関数の式が決まるので、説明変数から目的変数の確率が求められます。
そして、目的変数の確率が0.5以上であれば1、0.5未満であれば0と分類します。
これがロジスティック回帰分析の分析手法です。

レッスンは以上です。
いかがでしたでしょうか？
キノコードではわかりやすく飽きない動画づくりを意識しています。
今後はこのようなレッスン動画の配信を予定しています。
レッスンの新着通知が行きますので、是非チャンネル登録をお願いします。
それでは、また次の数式を使って理解編のレッスンでお会いしましょう。

参考文献

1. 永田 靖（1992）　『入門統計解析法』　日科技連
2. 平井　有三（2012）　『はじめてのパターン認識』　森北出版
3. 涌井良幸・涌井貞美（2016）　『身につくベイズ統計学』　技術評論社