こんにちは、キノコードです。
この動画では、株価がいくらになるかを予想する方法について解説をします。
ご自身で株式投資をしている方も多いのではないでしょうか。
みなさんは、どのように判断をして売り買いをしていらっしゃいますか?
株価が上がるか下がるかは、様々な要因があり、正しく予想することは非常に難しいことです。
とはいえ、投資銀行などでは、コンピュータが、人工知能による自動売買している部分が多いといわれています。
そして、コンピュータでの取引アルゴリズムの精度を高めるために、データサイエンティストによる研究が日々行われています。
同じように、機械学習で取引をしてみたいと思いませんか? ですが、株価の予測というテーマは、機械学習にチャレンジしてみるにはおもしろいテーマだと思います。
売り上げ予測や在庫予測など、ご自身のお仕事のテーマに転用いただければと思います。
前回の動画では、機械学習を使って、株価が上がるか下がるかを予測する方法を紹介しました。まだご覧になっていな方は、こちらも参考になさってください。
今回は、機械学習を使って、株価がいくらになるかを予測する方法を紹介します。
また、キノコードでは、ファイナンスのデータ分析やテクニカル分析の動画や、プログラミングに関する動画をたくさんアップしています。
チャンネル登録がまだの方は、新着通知も届きますので、ぜひチャンネル登録をお願いします。
それでは、レッスンスタートです。
レッスンで使ったファイルはこちら
キノクエストでアカウントの新規登録に進み、メール認証を完了します。
ログインした状態(プラン選択画面が表示されます)で下記のボタンをクリックしてください。
使用するデータと予測モデルについて
今回使用するデータは、実際の日経平均株価のデータです。
2018年1月〜2021年12月まで4年分のデータを使用します。データは、取引日毎の始値、終値、最高値、最安値、調整後終値、出来高がセットになっています。
2018年1月〜2020年12月の3年分のデータから予測モデルを作成し、2021年の金曜日の終値を予測するものとします。
そして、予測手法にはたくさんの手法がありますが、今回用いる分析手法は重回帰分析です。
重回帰分析で、株価がいくらになるのかを予測します。
重回帰分析とは、複数の説明変数から一つの目的変数を予測する分析手法です。一方で、一つの説明変数から一つの目的変数を予測する手法を単回帰分析といいます。重回帰分析や単回帰分析は、説明変数に対して目的変数を線形か線形に近い値で表すことができるため、線形回帰と呼ばれます。
例えば、部屋の数、駅からの距離、面積から家賃を予測するのが重回帰分析です。面積から家賃を予測するのが単回帰分析です。
単回帰分析については、詳しく解説した動画がありますのでそちらをご覧ください。
また、重回帰分析について解説した動画も準備中です。少々お待ちください。
重回帰分析は、複数の説明変数がどのくらい目的変数に対して影響があるかを重みづけし、このような関数で表すことができます。
それでは、実際にコードを書いてみましょう。
株価データを読み込み目的変数を追加
# ライブラリのインポート
from datetime import datetime, timedelta
import numpy as np
import pandas as pd
from pandas_datareader import data
import matplotlib.pyplot as plt
%matplotlib inlineまずは、使用するライブラリをインポートしましょう。
今回使用する日経平均株価のデータセットはpandas_datareaderより取得します。
pandas_datareaderにあるdataモジュールをインポートして、DataReaderメソッドを用います。
その他、必要なライブラリをまとめてインポートします。
# ワーニングを非表示にする設定(任意)
import warnings
warnings.simplefilter('ignore')# 最大表示行数の指定(任意:ここでは10行を指定)
pd.set_option('display.max_rows', 10)続けて、これらの設定は任意ですが、ワーニングを非表示にする設定、pandasの表示行数の設定をします。
それぞれ、この記述で設定することができます。
# pandas_datareaderを使って、2018年始から2021年末までの日経平均株価データの取得
start = '2018-01-01'
end = '2021-12-31'
data_master = data.DataReader('^N225', 'yahoo', start, end)
data_master| High | Low | Open | Close | Volume | Adj Close | |
|---|---|---|---|---|---|---|
| Date | ||||||
| 2018-01-04 | 23506.330078 | 23065.199219 | 23073.730469 | 23506.330078 | 102200000.0 | 23506.330078 |
| 2018-01-05 | 23730.470703 | 23520.519531 | 23643.000000 | 23714.529297 | 101900000.0 | 23714.529297 |
| 2018-01-09 | 23952.609375 | 23789.029297 | 23948.970703 | 23849.990234 | 94100000.0 | 23849.990234 |
| 2018-01-10 | 23864.759766 | 23755.449219 | 23832.810547 | 23788.199219 | 88800000.0 | 23788.199219 |
| 2018-01-11 | 23734.970703 | 23601.839844 | 23656.390625 | 23710.429688 | 83700000.0 | 23710.429688 |
| ... | ... | ... | ... | ... | ... | ... |
| 2021-12-24 | 28870.130859 | 28773.500000 | 28836.050781 | 28782.589844 | 35900000.0 | 28782.589844 |
| 2021-12-27 | 28805.279297 | 28658.820312 | 28786.330078 | 28676.460938 | 37500000.0 | 28676.460938 |
| 2021-12-28 | 29121.009766 | 28879.679688 | 28953.320312 | 29069.160156 | 47000000.0 | 29069.160156 |
| 2021-12-29 | 29106.279297 | 28729.609375 | 28995.730469 | 28906.880859 | 44700000.0 | 28906.880859 |
| 2021-12-30 | 28904.419922 | 28579.490234 | 28794.240234 | 28791.710938 | 40400000.0 | 28791.710938 |
974 rows × 6 columns
次に、pandas_datareaderを使用して、日経平均株価のデータを取得します。
開始日の2018年1月1日と終了日の2021年12月31日を、それぞれ、変数startとendに代入します。
pandas_datareaderのDataReaderメソッドを用いて、第1引数に日経平均株価のティッカーシンボル'^N225'、第2引数にデータソースの'yahoo'、第3引数に開始日の変数start、第4引数に終了日の変数endを渡します。ここで取得したデータをdata_masterに代入します。
data_masterを表示してみましょう。実行します。
データが取得できました。
# 曜日情報を追加(0:月曜日〜4:金曜日)
data_master['weekday'] = data_master.index.weekday
data_master| High | Low | Open | Close | Volume | Adj Close | weekday | |
|---|---|---|---|---|---|---|---|
| Date | |||||||
| 2018-01-04 | 23506.330078 | 23065.199219 | 23073.730469 | 23506.330078 | 102200000.0 | 23506.330078 | 3 |
| 2018-01-05 | 23730.470703 | 23520.519531 | 23643.000000 | 23714.529297 | 101900000.0 | 23714.529297 | 4 |
| 2018-01-09 | 23952.609375 | 23789.029297 | 23948.970703 | 23849.990234 | 94100000.0 | 23849.990234 | 1 |
| 2018-01-10 | 23864.759766 | 23755.449219 | 23832.810547 | 23788.199219 | 88800000.0 | 23788.199219 | 2 |
| 2018-01-11 | 23734.970703 | 23601.839844 | 23656.390625 | 23710.429688 | 83700000.0 | 23710.429688 | 3 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 2021-12-24 | 28870.130859 | 28773.500000 | 28836.050781 | 28782.589844 | 35900000.0 | 28782.589844 | 4 |
| 2021-12-27 | 28805.279297 | 28658.820312 | 28786.330078 | 28676.460938 | 37500000.0 | 28676.460938 | 0 |
| 2021-12-28 | 29121.009766 | 28879.679688 | 28953.320312 | 29069.160156 | 47000000.0 | 29069.160156 | 1 |
| 2021-12-29 | 29106.279297 | 28729.609375 | 28995.730469 | 28906.880859 | 44700000.0 | 28906.880859 | 2 |
| 2021-12-30 | 28904.419922 | 28579.490234 | 28794.240234 | 28791.710938 | 40400000.0 | 28791.710938 | 3 |
974 rows × 7 columns
インデックスが日付'Date'、カラムは、最高値'High'、最安値'Low'、始値'Open'、終値'Close'、出来高'Volume'、調整後終値'Adj Close'、の6個のデータフレームです。
indexの日付のデータを用いて'weekday'カラムを追加し、曜日の情報を作成しましょう。
表示してみましょう。
曜日'weekday'が追加できました。曜日は、月曜日を基準の0とした6までの数値で表されています。
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(data_master['Close'], label='Close', color='orange')
plt.xlabel('Date')
plt.ylabel('JPY')
plt.legend()
plt.show()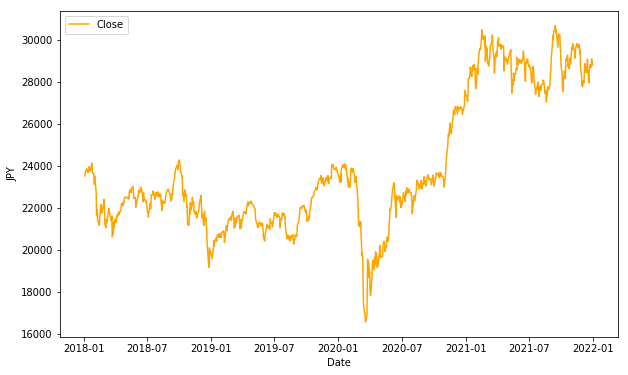
終値'Close'について、グラフを表示して確認してみましょう。
2018年1月から2020年1月頃まで、20000円から24000円の間を推移していますが、一旦17000円を下回り、その後28000円から30000円程度に上がっている傾向が確認できます。
説明変数の追加と目的変数の設定
次に、予測に影響しそうな目的変数を追加しましょう。
今回はファイナンス分析でよく使用される指標として、
- 移動平均
- 実体
- 終値の前日差分
を追加します。
# data_techinicalにデータをコピー
data_technical = data_master.copy()まず、データフレームdata_masterをpandasのcopyメソッドを使用し、新しいデータフレームdata_technicalにコピーします。
こうすることで元のデータを残しておくことができます。元のデータに目的変数を追加してしまうと、どの目的変数を採用するか検討する際に複雑になってしまいます。コピーしたデータフレームに目的変数を追加するとよいでしょう。
# 移動平均を追加
SMA1 = 5 #短期5日
SMA2 = 10 #中期10日
SMA3 = 15 #長期15日
data_technical['SMA1'] = data_technical['Close'].rolling(SMA1).mean() #短期移動平均の算出
data_technical['SMA2'] = data_technical['Close'].rolling(SMA2).mean() #中期移動平均の算出
data_technical['SMA3'] = data_technical['Close'].rolling(SMA3).mean() #長期移動平均の算出次に、移動平均を短期5日間、中期10日間、長期15日間の3種類を追加します。
それぞれ、変数SMA1、SMA2、SMA3に5、10、15を代入します。
データフレームdata_technicalに移動平均のカラム'SMA1'から'SMA3'を追加し、終値の移動平均の計算結果をそれぞれ代入します。移動平均は、pandasのrollingメソッドを使用すると簡単に計算ができます。引数に、それぞれの移動平均日数である変数SMA1からSMA3を指定します。
# 特徴量を描画して確認
plt.figure(figsize=(10, 6))
plt.plot(data_technical['Close'], label='Close', color='orange')
plt.plot(data_technical['SMA1'], label='SMA1', color='red')
plt.plot(data_technical['SMA2'], label='SMA2', color='blue')
plt.plot(data_technical['SMA3'], label='SMA3', color='green')
plt.xlabel('Date')
plt.ylabel('JPY')
plt.legend()
plt.show()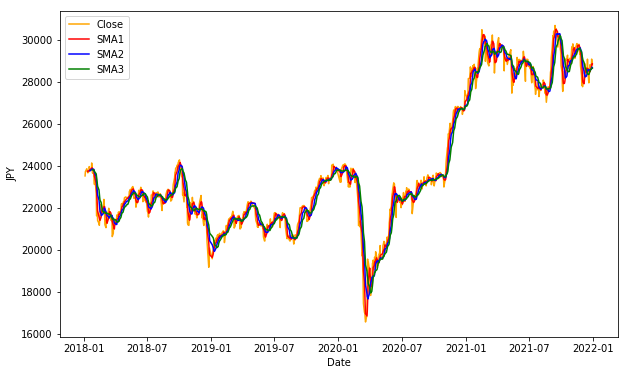
終値、3つの移動平均をグラフで表示してみましょう。
3本の移動平均線が追加されていることが確認できました。しかし、このままだと3本とも重なっていて違いが分かりにくいです。横軸の期間を一部指定することで、拡大して見てみましょう。
# 特徴量を描画して確認(x軸の拡大)
plt.figure(figsize=(10, 6))
plt.plot(data_technical['Close'], label='Close', color='orange')
plt.plot(data_technical['SMA1'], label='SMA1', color='red')
plt.plot(data_technical['SMA2'], label='SMA2', color='blue')
plt.plot(data_technical['SMA3'], label='SMA3', color='green')
plt.xlabel('Date')
plt.ylabel('JPY')
plt.legend()
xmin = datetime(2018,1,1)
xmax = datetime(2018,12,31)
plt.xlim([xmin,xmax])
plt.show()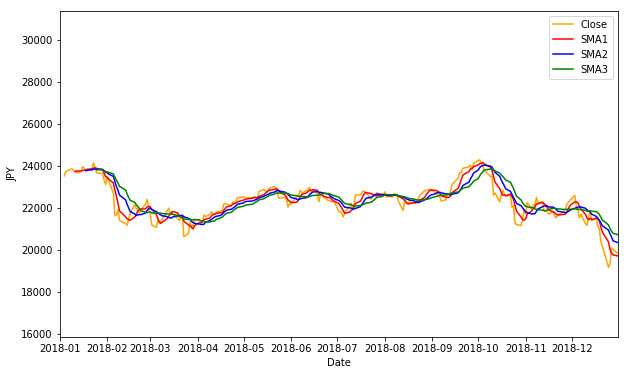
2018年の1月から12月までを表示してみます。X軸の範囲をxminとxmaxでそれぞれを指定します。実行します。
3本の移動平均線を確認できました。
また、移動平均を計算する際に初めの数日データが存在しないこともわかります。5日間の移動平均を計算する場合は、初めの4日は計算ができないため欠損値となります。同様に15日間の移動平均を計算する場合は、初めの14日間は欠損値となります。
# OpenとCloseの差分を実体Bodyとして計算
data_technical['Body'] = data_technical['Open'] - data_technical['Close']
# 前日終値との差分Close_diffを計算
data_technical['Close_diff'] = data_technical['Close'].diff(1)
# 目的変数となる翌日の終値Close_nextの追加
data_technical['Close_next'] = data_technical['Close'].shift(-1)
data_technical| High | Low | Open | Close | Volume | Adj Close | weekday | SMA1 | SMA2 | SMA3 | Body | Close_diff | Close_next | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Date | |||||||||||||
| 2018-01-04 | 23506.330078 | 23065.199219 | 23073.730469 | 23506.330078 | 102200000.0 | 23506.330078 | 3 | NaN | NaN | NaN | -432.599609 | NaN | 23714.529297 |
| 2018-01-05 | 23730.470703 | 23520.519531 | 23643.000000 | 23714.529297 | 101900000.0 | 23714.529297 | 4 | NaN | NaN | NaN | -71.529297 | 208.199219 | 23849.990234 |
| 2018-01-09 | 23952.609375 | 23789.029297 | 23948.970703 | 23849.990234 | 94100000.0 | 23849.990234 | 1 | NaN | NaN | NaN | 98.980469 | 135.460938 | 23788.199219 |
| 2018-01-10 | 23864.759766 | 23755.449219 | 23832.810547 | 23788.199219 | 88800000.0 | 23788.199219 | 2 | NaN | NaN | NaN | 44.611328 | -61.791016 | 23710.429688 |
| 2018-01-11 | 23734.970703 | 23601.839844 | 23656.390625 | 23710.429688 | 83700000.0 | 23710.429688 | 3 | 23713.895703 | NaN | NaN | -54.039062 | -77.769531 | 23653.820312 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2021-12-24 | 28870.130859 | 28773.500000 | 28836.050781 | 28782.589844 | 35900000.0 | 28782.589844 | 4 | 28519.714062 | 28574.342187 | 28543.350000 | 53.460938 | -15.779297 | 28676.460938 |
| 2021-12-27 | 28805.279297 | 28658.820312 | 28786.330078 | 28676.460938 | 37500000.0 | 28676.460938 | 0 | 28667.444141 | 28577.939258 | 28593.289453 | 109.869141 | -106.128906 | 29069.160156 |
| 2021-12-28 | 29121.009766 | 28879.679688 | 28953.320312 | 29069.160156 | 47000000.0 | 29069.160156 | 1 | 28777.758203 | 28641.591211 | 28634.193490 | -115.839844 | 392.699219 | 28906.880859 |
| 2021-12-29 | 29106.279297 | 28729.609375 | 28995.730469 | 28906.880859 | 44700000.0 | 28906.880859 | 2 | 28846.692188 | 28686.307227 | 28637.277604 | 88.849609 | -162.279297 | 28791.710938 |
| 2021-12-30 | 28904.419922 | 28579.490234 | 28794.240234 | 28791.710938 | 40400000.0 | 28791.710938 | 3 | 28845.360547 | 28658.846289 | 28641.693620 | 2.529297 | -115.169922 | NaN |
974 rows × 13 columns
次に、'Body'を追加します。これは、ローソク足でいう実体です。始値と終値の差分を計算します。
また、前日終値との差分'Close_diff'を追加します。これは、diffメソッドで計算できます。
最後に、目的変数の翌日終値'Close_next'を追加しましょう。shiftメソッドで1日前にずらすことで、翌日の終値を計算します。
表示して確認してみましょう。実行します。
前日終値との差分'Close_diff'は初めのデータが欠損値となっており、翌日の終値'Close_next'は最後のデータが欠損値となっていることが確認できます。
# 欠損値がある行を削除
data_technical = data_technical.dropna(how='any')
data_technical| High | Low | Open | Close | Volume | Adj Close | weekday | SMA1 | SMA2 | SMA3 | Body | Close_diff | Close_next | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Date | |||||||||||||
| 2018-01-25 | 23828.400391 | 23649.029297 | 23750.650391 | 23669.490234 | 81500000.0 | 23669.490234 | 3 | 23871.762109 | 23831.103125 | 23792.033984 | 81.160156 | -271.289062 | 23631.880859 |
| 2018-01-26 | 23797.960938 | 23592.279297 | 23757.339844 | 23631.880859 | 87200000.0 | 23631.880859 | 4 | 23836.526172 | 23828.909180 | 23800.404036 | 125.458984 | -37.609375 | 23629.339844 |
| 2018-01-29 | 23787.230469 | 23580.169922 | 23707.140625 | 23629.339844 | 68800000.0 | 23629.339844 | 0 | 23799.128125 | 23820.355078 | 23794.724740 | 77.800781 | -2.541016 | 23291.970703 |
| 2018-01-30 | 23581.980469 | 23233.369141 | 23559.330078 | 23291.970703 | 88800000.0 | 23291.970703 | 1 | 23632.692188 | 23754.371094 | 23757.523438 | 267.359375 | -337.369141 | 23098.289062 |
| 2018-01-31 | 23375.380859 | 23092.849609 | 23205.230469 | 23098.289062 | 99800000.0 | 23098.289062 | 2 | 23464.194141 | 23677.366016 | 23711.529427 | 106.941406 | -193.681641 | 23486.109375 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2021-12-23 | 28798.369141 | 28640.150391 | 28703.009766 | 28798.369141 | 43600000.0 | 28798.369141 | 3 | 28472.332031 | 28539.860156 | 28493.148698 | -95.359375 | 236.158203 | 28782.589844 |
| 2021-12-24 | 28870.130859 | 28773.500000 | 28836.050781 | 28782.589844 | 35900000.0 | 28782.589844 | 4 | 28519.714062 | 28574.342187 | 28543.350000 | 53.460938 | -15.779297 | 28676.460938 |
| 2021-12-27 | 28805.279297 | 28658.820312 | 28786.330078 | 28676.460938 | 37500000.0 | 28676.460938 | 0 | 28667.444141 | 28577.939258 | 28593.289453 | 109.869141 | -106.128906 | 29069.160156 |
| 2021-12-28 | 29121.009766 | 28879.679688 | 28953.320312 | 29069.160156 | 47000000.0 | 29069.160156 | 1 | 28777.758203 | 28641.591211 | 28634.193490 | -115.839844 | 392.699219 | 28906.880859 |
| 2021-12-29 | 29106.279297 | 28729.609375 | 28995.730469 | 28906.880859 | 44700000.0 | 28906.880859 | 2 | 28846.692188 | 28686.307227 | 28637.277604 | 88.849609 | -162.279297 | 28791.710938 |
959 rows × 13 columns
それでは、欠損値を含む行を削除しましょう。欠損値の削除は、dropnaメソッドを使用します。
欠損値があるか、isnullメソッドで件数を確認してみましょう。実行します。
件数が0件のため、欠損値を削除できたことを確認できました。
# 木曜日のデータを抜き出す
data_technical = data_technical[data_technical['weekday'] == 3]
data_technical| High | Low | Open | Close | Volume | Adj Close | weekday | SMA1 | SMA2 | SMA3 | Body | Close_diff | Close_next | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Date | |||||||||||||
| 2018-01-25 | 23828.400391 | 23649.029297 | 23750.650391 | 23669.490234 | 81500000.0 | 23669.490234 | 3 | 23871.762109 | 23831.103125 | 23792.033984 | 81.160156 | -271.289062 | 23631.880859 |
| 2018-02-01 | 23492.769531 | 23211.119141 | 23276.099609 | 23486.109375 | 101800000.0 | 23486.109375 | 3 | 23427.517969 | 23649.640039 | 23696.574740 | -210.009766 | 387.820312 | 23274.529297 |
| 2018-02-08 | 21977.029297 | 21649.699219 | 21721.570312 | 21890.859375 | 104700000.0 | 21890.859375 | 3 | 22220.615625 | 22824.066797 | 23173.298568 | -169.289062 | 245.490234 | 21382.619141 |
| 2018-02-15 | 21578.990234 | 21308.919922 | 21384.099609 | 21464.980469 | 86400000.0 | 21464.980469 | 3 | 21427.461719 | 21983.563672 | 22477.107161 | -80.880859 | 310.810547 | 21720.250000 |
| 2018-02-22 | 21799.400391 | 21626.849609 | 21789.880859 | 21736.439453 | 77300000.0 | 21736.439453 | 3 | 21900.362109 | 21663.911914 | 21955.829818 | 53.441406 | -234.371094 | 21892.779297 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2021-11-25 | 29570.419922 | 29444.449219 | 29469.650391 | 29499.279297 | 50700000.0 | 29499.279297 | 3 | 29584.115625 | 29608.165820 | 29559.125911 | -29.628906 | 196.619141 | 28751.619141 |
| 2021-12-02 | 27938.550781 | 27644.960938 | 27716.199219 | 27753.369141 | 77400000.0 | 27753.369141 | 3 | 28109.257422 | 28846.686523 | 29108.529687 | -37.169922 | -182.250000 | 28029.570312 |
| 2021-12-09 | 28908.289062 | 28725.470703 | 28827.320312 | 28725.470703 | 54400000.0 | 28725.470703 | 3 | 28399.725781 | 28254.491602 | 28697.699609 | 101.849609 | -135.148438 | 28437.769531 |
| 2021-12-16 | 29070.080078 | 28782.189453 | 28868.369141 | 29066.320312 | 60300000.0 | 29066.320312 | 3 | 28607.388281 | 28503.557031 | 28372.123828 | -197.951172 | 606.599609 | 28545.679688 |
| 2021-12-23 | 28798.369141 | 28640.150391 | 28703.009766 | 28798.369141 | 43600000.0 | 28798.369141 | 3 | 28472.332031 | 28539.860156 | 28493.148698 | -95.359375 | 236.158203 | 28782.589844 |
193 rows × 13 columns
次に、予測に使用する木曜日のデータのみを抜き出します。木曜日はweekdayが3です。実行します。
木曜日だけのデータを抽出できました。
# 必要なカラムを抽出
data_technical = data_technical[['High', 'Low', 'Open', 'Close', 'Body',
'Close_diff', 'SMA1', 'SMA2', 'SMA3', 'Close_next']]
data_technical| High | Low | Open | Close | Body | Close_diff | SMA1 | SMA2 | SMA3 | Close_next | |
|---|---|---|---|---|---|---|---|---|---|---|
| Date | ||||||||||
| 2018-01-25 | 23828.400391 | 23649.029297 | 23750.650391 | 23669.490234 | 81.160156 | -271.289062 | 23871.762109 | 23831.103125 | 23792.033984 | 23631.880859 |
| 2018-02-01 | 23492.769531 | 23211.119141 | 23276.099609 | 23486.109375 | -210.009766 | 387.820312 | 23427.517969 | 23649.640039 | 23696.574740 | 23274.529297 |
| 2018-02-08 | 21977.029297 | 21649.699219 | 21721.570312 | 21890.859375 | -169.289062 | 245.490234 | 22220.615625 | 22824.066797 | 23173.298568 | 21382.619141 |
| 2018-02-15 | 21578.990234 | 21308.919922 | 21384.099609 | 21464.980469 | -80.880859 | 310.810547 | 21427.461719 | 21983.563672 | 22477.107161 | 21720.250000 |
| 2018-02-22 | 21799.400391 | 21626.849609 | 21789.880859 | 21736.439453 | 53.441406 | -234.371094 | 21900.362109 | 21663.911914 | 21955.829818 | 21892.779297 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2021-11-25 | 29570.419922 | 29444.449219 | 29469.650391 | 29499.279297 | -29.628906 | 196.619141 | 29584.115625 | 29608.165820 | 29559.125911 | 28751.619141 |
| 2021-12-02 | 27938.550781 | 27644.960938 | 27716.199219 | 27753.369141 | -37.169922 | -182.250000 | 28109.257422 | 28846.686523 | 29108.529687 | 28029.570312 |
| 2021-12-09 | 28908.289062 | 28725.470703 | 28827.320312 | 28725.470703 | 101.849609 | -135.148438 | 28399.725781 | 28254.491602 | 28697.699609 | 28437.769531 |
| 2021-12-16 | 29070.080078 | 28782.189453 | 28868.369141 | 29066.320312 | -197.951172 | 606.599609 | 28607.388281 | 28503.557031 | 28372.123828 | 28545.679688 |
| 2021-12-23 | 28798.369141 | 28640.150391 | 28703.009766 | 28798.369141 | -95.359375 | 236.158203 | 28472.332031 | 28539.860156 | 28493.148698 | 28782.589844 |
193 rows × 10 columns
最後に、必要なカラムだけを抽出します。実行します。
ここまでで、データの準備は完了しました。
学習用データとテストデータに分割
次に、予測モデルを作成しましょう。
まず、データセットを学習用データとテストデータに分割します。学習データからモデルを作成し、作成したモデルでテストデータの予測をします。
今回のデータでは、2018年1月から2020年12月までの3年分のデータを学習用データ、2021年1月から12月までの1年分をテストデータとしします。
# 2018年〜2020年を学習用データとする
train = data_technical['2018-01-01' : '2020-12-31']
train| High | Low | Open | Close | Body | Close_diff | SMA1 | SMA2 | SMA3 | Close_next | |
|---|---|---|---|---|---|---|---|---|---|---|
| Date | ||||||||||
| 2018-01-25 | 23828.400391 | 23649.029297 | 23750.650391 | 23669.490234 | 81.160156 | -271.289062 | 23871.762109 | 23831.103125 | 23792.033984 | 23631.880859 |
| 2018-02-01 | 23492.769531 | 23211.119141 | 23276.099609 | 23486.109375 | -210.009766 | 387.820312 | 23427.517969 | 23649.640039 | 23696.574740 | 23274.529297 |
| 2018-02-08 | 21977.029297 | 21649.699219 | 21721.570312 | 21890.859375 | -169.289062 | 245.490234 | 22220.615625 | 22824.066797 | 23173.298568 | 21382.619141 |
| 2018-02-15 | 21578.990234 | 21308.919922 | 21384.099609 | 21464.980469 | -80.880859 | 310.810547 | 21427.461719 | 21983.563672 | 22477.107161 | 21720.250000 |
| 2018-02-22 | 21799.400391 | 21626.849609 | 21789.880859 | 21736.439453 | 53.441406 | -234.371094 | 21900.362109 | 21663.911914 | 21955.829818 | 21892.779297 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2020-11-26 | 26560.029297 | 26255.470703 | 26255.470703 | 26537.310547 | -281.839844 | 240.451172 | 26032.293750 | 25871.790820 | 25482.896484 | 26644.710938 |
| 2020-12-03 | 26868.089844 | 26719.230469 | 26740.300781 | 26809.369141 | -69.068359 | 8.388672 | 26695.243750 | 26363.768750 | 26146.275130 | 26751.240234 |
| 2020-12-10 | 26852.769531 | 26639.980469 | 26688.500000 | 26756.240234 | -67.740234 | -61.699219 | 26667.987891 | 26681.615820 | 26465.175130 | 26652.519531 |
| 2020-12-17 | 26843.050781 | 26676.279297 | 26744.500000 | 26806.669922 | -62.169922 | 49.269531 | 26727.373828 | 26697.680859 | 26696.868490 | 26763.390625 |
| 2020-12-24 | 26764.529297 | 26605.259766 | 26635.109375 | 26668.349609 | -33.240234 | 143.560547 | 26621.467969 | 26674.420898 | 26672.276562 | 26656.609375 |
146 rows × 10 columns
では、2018年1月1日から2020年12月31日までのデータを、学習用データとして変数trainに代入します。
表示してみましょう。
trainには、2018年から2020年までのデータが格納されていることが確認できます。
# 2021年をテストデータとする
test = data_technical['2021-01-01' :]
test| High | Low | Open | Close | Body | Close_diff | SMA1 | SMA2 | SMA3 | Close_next | |
|---|---|---|---|---|---|---|---|---|---|---|
| Date | ||||||||||
| 2021-01-07 | 27624.730469 | 27340.460938 | 27340.460938 | 27490.130859 | -149.669922 | 434.191406 | 27281.450391 | 27067.917969 | 26943.830078 | 28139.029297 |
| 2021-01-14 | 28979.529297 | 28411.580078 | 28442.730469 | 28698.259766 | -255.529297 | 241.669922 | 28189.669922 | 27743.362109 | 27371.585938 | 28519.179688 |
| 2021-01-21 | 28846.150391 | 28677.609375 | 28710.410156 | 28756.859375 | -46.449219 | 233.599609 | 28534.994141 | 28362.332031 | 28007.239453 | 28631.449219 |
| 2021-01-28 | 28360.480469 | 27975.849609 | 28169.269531 | 28197.419922 | -28.150391 | -437.791016 | 28566.509766 | 28550.751953 | 28430.391276 | 27663.390625 |
| 2021-02-04 | 28600.220703 | 28325.890625 | 28557.460938 | 28341.949219 | 215.511719 | -304.550781 | 28221.012109 | 28393.760937 | 28440.838672 | 28779.189453 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2021-11-25 | 29570.419922 | 29444.449219 | 29469.650391 | 29499.279297 | -29.628906 | 196.619141 | 29584.115625 | 29608.165820 | 29559.125911 | 28751.619141 |
| 2021-12-02 | 27938.550781 | 27644.960938 | 27716.199219 | 27753.369141 | -37.169922 | -182.250000 | 28109.257422 | 28846.686523 | 29108.529687 | 28029.570312 |
| 2021-12-09 | 28908.289062 | 28725.470703 | 28827.320312 | 28725.470703 | 101.849609 | -135.148438 | 28399.725781 | 28254.491602 | 28697.699609 | 28437.769531 |
| 2021-12-16 | 29070.080078 | 28782.189453 | 28868.369141 | 29066.320312 | -197.951172 | 606.599609 | 28607.388281 | 28503.557031 | 28372.123828 | 28545.679688 |
| 2021-12-23 | 28798.369141 | 28640.150391 | 28703.009766 | 28798.369141 | -95.359375 | 236.158203 | 28472.332031 | 28539.860156 | 28493.148698 | 28782.589844 |
47 rows × 10 columns
同様に、2021年1月1日以降のデータをテストデータとしてtestに代入します。
表示してみましょう。
testには、2021年のデータが格納されていることが確認できます。
# 学習用データとテストデータそれぞれを説明変数と目的変数に分離する
X_train = train.drop(columns=['Close_next']) #学習用データ説明変数
y_train = train['Close_next'] #学習用データ目的変数
X_test = test.drop(columns=['Close_next']) #テストデータ説明変数
y_test = test['Close_next'] #テストデータ目的変数続いて、学習用データとテストデータを、それぞれ説明変数と目的変数に分割します。
ここでは、目的変数は翌日の株価終値'Close_next'となるため、それ以外が説明変数ということになります。
学習用データの説明変数をX_train、学習用データの目的変数をy_trainに代入します。同様に、テストデータの説明変数をX_test、テストデータの目的変数をy_testとします。
実行します。
予測モデルを作成する準備ができました。
モデル作成と精度検証
それでは、予測モデルを作成しましょう。
予測モデルを作成する際には、実際に使用できるモデルかどうかの、予測精度を検討する必要があります。この時、交差検証を行うことが有効と考えられます。
交差検証とは、学習用データを学習データと検証データに分割し、学習データと検証データの組み合わせを変えながらモデルの学習と予想を繰り返し行い、精度検証を行うというものです。
交差検証のやり方は様々ありますが、今回の様にデータが日付順に並んだ時系列データを用いて、過去のデータから未来を予測する場合は、時系列交差検証を行うことがあります。
今回は、学習データを時系列に5分割し、データの組み合わせを変えて合計4回のモデル作成から精度検証を繰り返し行います。
# 線形回帰モデルのLinearRegressionをインポート
from sklearn.linear_model import LinearRegression
# 時系列分割のためTimeSeriesSplitのインポート
from sklearn.model_selection import TimeSeriesSplit
# 予測精度検証のためMSEをインポート
from sklearn.metrics import mean_squared_error as msescikit-learn で重回帰分析を行う場合は、LinearRegression クラスを使用するので、これをインポートします。時系列交差検証を行うためにデータ分割を行うTimeSeriesSplitと、予測精度評価を行うためのmseをインポートします。実行します。
# 時系列分割交差検証
valid_scores = []
tscv = TimeSeriesSplit(n_splits=4)
for fold, (train_indices, valid_indices) in enumerate(tscv.split(X_train)):
X_train_cv, X_valid_cv = X_train.iloc[train_indices], X_train.iloc[valid_indices]
y_train_cv, y_valid_cv = y_train.iloc[train_indices], y_train.iloc[valid_indices]
# 線形回帰モデルのインスタンス化
model = LinearRegression()
# モデル学習
model.fit(X_train_cv, y_train_cv)
# 予測
y_valid_pred = model.predict(X_valid_cv)
# 予測精度(RMSE)の算出
score = np.sqrt(mse(y_valid_cv, y_valid_pred))
# 予測精度スコアをリストに格納
valid_scores.append(score)まず、交差検証結果を格納するために、空のリストvalid_scoresを定義します。
次に、TimeSeriesSplitをインスタンス化します。
交差検証はfor文を用いて次のような流れで実行します。
まず、交差検証用のデータセットを作成します。学習データと検証データの説明変数、目的変数をそれぞれ設定します。
次に、線形回帰モデルをインスタンス化します。続けてモデル学習をし、このモデルで予測をします。
そして、予測結果の精度を検証します。ちなみに、予測精度を確認するために計算されたMSEは、誤差を2乗したものです。これをわかりやすくするために、平方根で計算したものがRMSEです。平均平方二乗誤差とも言います。
RMSEを用いることで、予測した値が正解の値からどの程度ずれているのかを確認しやすくなります。また、この指標は数字が小さいほど予測精度が高いことを示します。
最後に予測精度をリストに格納します。
実行してみましょう。
RMSEで精度確認
print(f'valid_scores: {valid_scores}')
cv_score = np.mean(valid_scores)
print(f'CV score: {cv_score}')valid_scores: [325.3625074145673, 169.61507596829318, 413.7658021675662, 201.0198662362686]
CV score: 277.4408129466738では、valid_scoresを表示して確認します。
このような結果になりました。
今回作成したモデルは、20000〜30000円の株価に対して、おおよそ300円の誤差で予測できると考えられます。
2021年金曜日の株価を前日木曜のデータから予測
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
score = np.sqrt(mse(y_test, y_pred))
print(f'RMSE: {score}')RMSE: 435.1219386786387先ほどのモデルを使用して、2021年の金曜日の株価を予測してみましょう。ここでは、先ほど作成した学習データとテストデータを使用します。
手順はこのように簡単です。
まず、線形回帰モデル(LinearRegression)のインスタンス化をします。
次に、学習データに対して線形回帰モデルで学習をします。第一引数には2018年〜2020年のデータの説明変数、第二引数には目的変数を指定します。
続けて、テストデータの説明変数を用いて、金曜日の株価を予測します。
最後に、予測した結果のy_predと実際の値であるテストデータの目的変数y_testから、予測精度のRMSEを算出します。
そして結果を表示しましょう。実行します。
RMSEはこのようになりました。交差検証の値よりも悪化したことがわかります。
可視化で予測と実際の値を確認
# 実際のデータと予測データをデータフレームにまとめる
df_result = test[['Close_next']]
df_result['Close_pred'] = y_pred
df_result| Close_next | Close_pred | |
|---|---|---|
| Date | ||
| 2021-01-07 | 28139.029297 | 27314.375717 |
| 2021-01-14 | 28519.179688 | 28621.255877 |
| 2021-01-21 | 28631.449219 | 28632.033099 |
| 2021-01-28 | 27663.390625 | 28031.227826 |
| 2021-02-04 | 28779.189453 | 28333.488693 |
| ... | ... | ... |
| 2021-11-25 | 28751.619141 | 29257.130866 |
| 2021-12-02 | 28029.570312 | 27456.390133 |
| 2021-12-09 | 28437.769531 | 28781.063265 |
| 2021-12-16 | 28545.679688 | 28930.344135 |
| 2021-12-23 | 28782.589844 | 28717.191783 |
47 rows × 2 columns
予測した値と実際の値がどの様になっているのか、目的変数だけをグラフにして確認してみましょう。
まず、実際のデータと予測データをデータフーレムdf_resultにまとめます。
実行します。
このようなデータフレームです。
# 実際のデータと予測データの比較グラフ作成
plt.figure(figsize=(10, 6))
plt.plot(df_result[['Close_next', 'Close_pred']])
plt.plot(df_result['Close_next'], label='Close_next', color='orange')
plt.plot(df_result['Close_pred'], label='Close_pred', color='blue')
plt.xlabel('Date')
plt.ylabel('JPY')
xmin = df_result.index.min()
xmax = df_result.index.max()
plt.legend()
plt.show()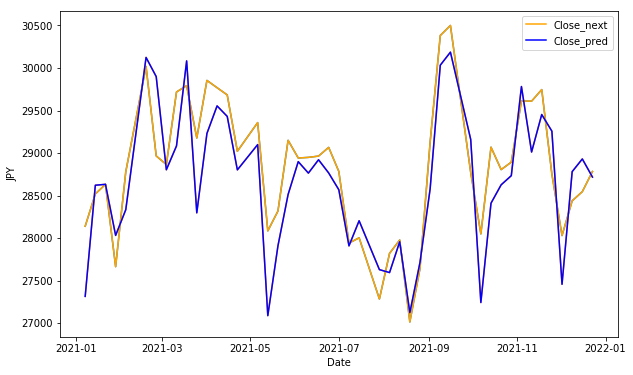
df_resultのグラフを描画してみます。
実際の値をオレンジ、予測した値を青の線で表示してみましょう。
株価の変動に対して、大まかな傾向は捉えていそうです
# 誤差を算出
df_result['diff'] = df_result['Close_pred'] - df_result['Close_next']今度は、どの部分の乖離が大きいのかを確認するために、誤差だけをグラフにしてみましょう。
誤差は予測した値と実際の値の差分で計算します。赤い線のグラフにしましょう。また、誤差の目安を750円としてY軸に補助線を追加します。実行します。
# 誤差のグラフ作成
plt.figure(figsize=(10, 6))
plt.plot(df_result[['diff']])
plt.plot(df_result['diff'], label='diff', color='red')
plt.xlabel('Date')
plt.ylabel('error')
plt.hlines(0, xmin, xmax, color='gray', linestyle='--')
plt.hlines(750, xmin, xmax, color='gray', linestyle=':')
plt.hlines(-750, xmin, xmax, color='gray', linestyle=':')
plt.legend()
plt.show()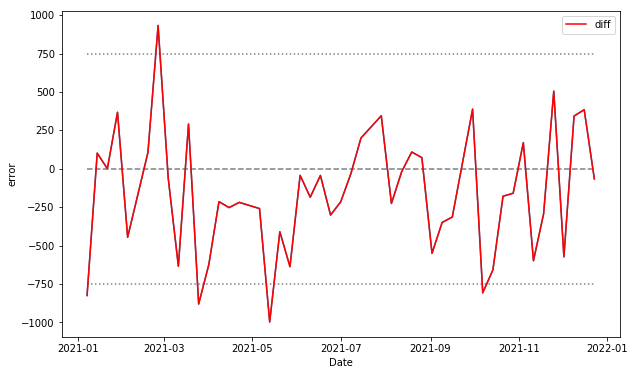
では、誤差が大きかったところに注目して見てみましょう
どの部分も実際の値段が直前に大きく下に変動していることがわかります。
ここでは実際の値段よりも予測値が高い傾向ですが、他のこれらは、実際の変動よりも低い値段で予測していることがわかります。
こうして見ると、今回作成したモデルは、株価が下がる場合に誤差が大きくなる可能性があると考えられます。
つまり、この様な傾向を上手く捉えて予測モデルを改善することで、精度を向上させられると期待できます。
モデルの精度向上の方法としては、
- 説明変数の見直し
- 学習データ期間の見直し
- 予測モデルの見直し
などを行うことが有効です。説明変数については、ファイナンスデータのテクニカル分析を説明した動画の中でいくつか紹介しています。ぜひこちらも参考になさってみてください。
予測モデルの係数と切片を確認
# 予測モデルの係数を確認
coef = pd.DataFrame(model.coef_) # データフレームの作成
coef.index = X_train.columns # 項目名をインデックスに設定
coef| 0 | |
|---|---|
| High | -2.484113e-01 |
| Low | -9.234009e-02 |
| Open | 3.949628e+10 |
| Close | -3.949628e+10 |
| Body | -3.949628e+10 |
| Close_diff | -2.587902e-01 |
| SMA1 | -2.694505e-01 |
| SMA2 | -1.519415e-01 |
| SMA3 | 4.854844e-02 |
さて、線形回帰モデルは、このような関数で予測値を表すことが可能です。
予測値 =A1×(説明変数1)+A2×(説明変数2)+・・・+An×(説明変数n)+K<
今回作成したモデルに対して、これらの値を確認してみます。
まず、係数は作成したモデルに対してcoef_メソッドで取得できます。ただし、これらがどの特徴量に紐づいているのかわかりにくいため、データフレームにしてみます。説明変数をインデックスにして表示してみましょう。
このように、説明変数に対する係数が表示されました。
# 予測モデルの切片を確認
model.intercept_409.8866450575515次に、切片です。intercept_メソッドで取得できます。実行します。
この関数を使って予測をした、ということです。
ここで、1点注意いただきたいのは、各説明変数の係数の大きさが相関の強さを示さない点です。
理由は、学習データの各説明変数ごとの分布が揃っていない為です。
# X_train基本統計量の確認
X_train.describe()| High | Low | Open | Close | Body | Close_diff | SMA1 | SMA2 | SMA3 | |
|---|---|---|---|---|---|---|---|---|---|
| count | 146.000000 | 146.000000 | 146.000000 | 146.000000 | 146.000000 | 146.000000 | 146.000000 | 146.000000 | 146.000000 |
| mean | 22298.102686 | 22065.494843 | 22202.529083 | 22174.560721 | 27.968362 | -23.304661 | 22173.247346 | 22164.036962 | 22154.239021 |
| std | 1559.027597 | 1602.983382 | 1558.689896 | 1593.250387 | 162.247579 | 265.426045 | 1548.152452 | 1500.769909 | 1451.165968 |
| min | 17160.970703 | 16358.190430 | 16995.769531 | 16552.830078 | -371.429688 | -915.179688 | 16944.800000 | 17647.499023 | 17983.368750 |
| 25% | 21488.967773 | 21287.489746 | 21404.336914 | 21348.322754 | -68.228027 | -168.834473 | 21279.394238 | 21398.351172 | 21356.857747 |
| 50% | 22285.825195 | 22065.250000 | 22189.254883 | 22191.609375 | 21.565430 | -2.640625 | 22177.097070 | 22088.985742 | 22103.505404 |
| 75% | 23203.060547 | 22888.586914 | 23110.392090 | 23023.372559 | 114.844238 | 124.198730 | 23138.541797 | 23093.306494 | 23126.927311 |
| max | 26868.089844 | 26719.230469 | 26744.500000 | 26809.369141 | 570.169922 | 750.558594 | 26727.373828 | 26697.680859 | 26696.868490 |
では、説明変数の分布を確認するために、モデルの学習に使用したX_trainの基本統計量を確認しましょう。
標準偏差stdを見ると、小さいもので実体'Body'の162に対して、大きいもので最安値'Low'の1602というように、説明変数間でばらつきに差があることがわかります。
原因は、データのスケールが異なることにあります。より影響の度合いを考慮したい場合は、データを標準化するとよいでしょう。
エンディング
いかがでしたでしょうか?
今回は重回帰分析での予測方法について、ファイナンスデータを使って説明しました。
重回帰分析については、別の動画で詳しく説明します。もう少々お待ちくださいませ。
また、キノコードではわかりやすく見飽きない動画作成を心がけています。
チャンネル登録がまだの方は、新着通知も届きますので、ぜひチャンネル登録をお願いします。それでは次のレッスンでお会いしましょう。




