こんにちはキノコードです。
これまでPythonを使った株価のデータ分析や、テクニカル分析について動画を出してきました。
これらの動画を⾒て学習していただければ、証券会社の提供ツールに縛られず、株価の分析をしていただけるはずです。
⼀⽅で、この分析結果を元に、株式の売買の意思決定を⾏うのはあなた⾃⾝です。
分析結果は意思決定の役に⽴ちますが、⾃分の感情などが意思決定に影響を与えてしまいます。 そのため、感情が再現性を阻害する一つになることもあります。
それでは、人工知能で予測した価格を元に取引をするのはどうでしょう?
感情に関わらず、定量的な判断ができますよね。
現在、投資銀行などでは、株や為替の取引で⼈間のトレーダーではなく、コンピュータが株式を⾃動売買している部分が多いといわれています。
そして取引のアルゴリズムの精度を⾼めるため、データサイエンティストによる研究が⽇夜⾏われています。
今回のレッスンでは、こうした機械学習による株価の予測について、基本的な⼿法のひとつを説明します。
ただし、Pythonの知識がある方、ある程度の機械学習に対する知識がある方に向けて説明をしています。
機械学習をイチから理解したい方やもっと詳しく学習しいたい方は、「人工知能開発レッスン」を用意しておりますので、そちらをご覧ください。
単回帰分析の次はロジスティック回帰や決定木、データの前処理方法などを準備しております。
また株価の予測だけでなく、過去の売り上げデータから、将来需要が上がるか、下がるかといった予測を⾏う場⾯でも、今回の学習内容を活⽤できます。
そのため会社で時系列のデータを使った分析をされる⽅にも役⽴つ内容になっています。
基本的な株価の分析の⽅法や、分析に使⽤するpandasの使い⽅を知りたい⽅は、 こちらの動画もご覧ください。
またチャンネル登録がまだの⽅は、チャンネルがどこに⾏ったか分からなくならないように、是⾮チャンネル登録をお願いします。
Python学習サービス「キノクエスト」のご紹介
キノコードでは、Pythonを習得するためのPython学習サービス「キノクエスト」を運営しています。
キノクエストには、学習カリキュラムがあり、学習順番に悩むことなく学習を進められます。
月額1,990円と本1冊分の値段です。
キノクエストの特徴は下記の通りです。
・Python学習をしている仲間が集まるコミュニティがある
・1000問以上の問題を解いてプログラミングを習得
・環境構築不要ですぐに始められる
・動画と連動しているので、インプットもできる。
・月額1,990円で、コミュニティもセット
キノクエストを詳しく知りたい方は、紹介ページをご覧ください。
▼キノクエストの紹介ページはこちら▼
https://kino-code.com/kq_service_a/
それでは解説に入ります。
株価データを読み込み目的変数を追加する
pandasをpdという名前でインポートします。
pandasのread_csvメソッドを用いて、ファイルを読み込みdfに格納します。使用するデータセットは'finance_dataset.csv'です。
そしてdfを表示します。
# pandasのインポート
import pandas as pd
# データの読み込み
df = pd.read_csv('finance_dataset.csv')
# データフレームの表示
df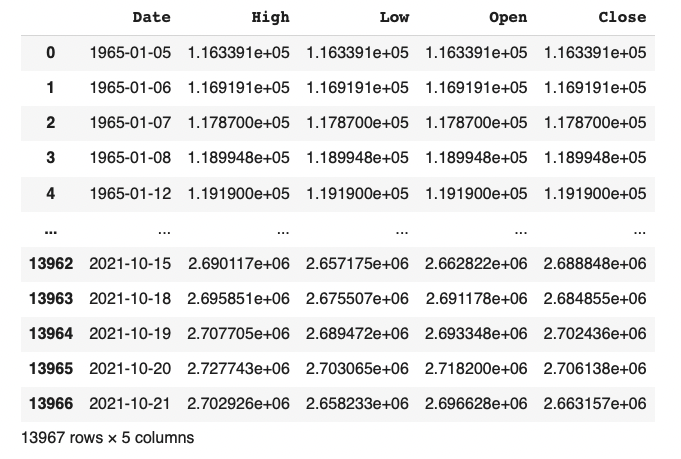
インデックスが0から13966までの連番で、カラムに
日付('Date')、最高値('High')、最安値('Low')、始値('Open')、終値('Close')が設定されたデータフレームである事が確認できます。
日付('Date)は1965年1月5日から2021年10月21日までとなっています。
後に詳しく説明を行いますが、予測モデル作成に対して、目的変数の追加や、週ごとにデータを纏める必要があります。
そのために、曜日情報や初めの週を基準として何週目となるか等の情報と、今回の目的変数である木曜日の終値から翌日金曜日の始値が上がるかどうかの’Up’(上がる場合は'1',同じ又は下がる場合は'0')を追加していきます。
次に、infoメソッドを用いて、欠損値の有無やカラムのデータ型の確認を行います。
# 各カラムの詳細確認
df.info()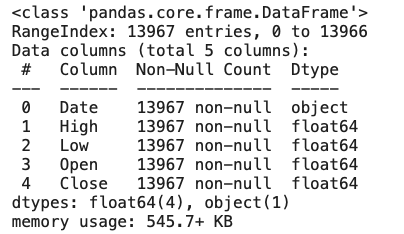
各カラム欠損値なしである事がわかります。
日付('Date')が’object'型となっています。今回の様な時系列データを用いる際には、'datetime64'型を用いる方が利便性が高い為、pandasの'to_datetime'メソッドを用いてデータ型の変換を行います。
# Dateのデータ型をを'datetime'型へ変更
df['Date'] = pd.to_datetime(df['Date'])
df.info()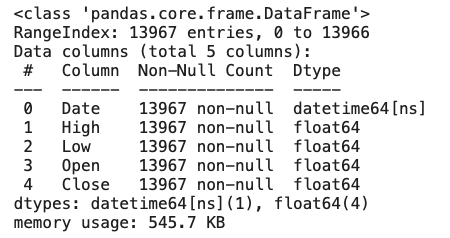
'Date'のカラムが'object'型から'datetime64'型へ代わっていることが確認できます。
次に曜日情報のカラムを追加します。'datetime64'型は'dt.weekday'メソッドを用いて、曜日情報を取得する事ができます。月曜日を0として連番の数字を設定されます。実行結果をdfに'weekday'カラムを追加して入力し、実行結果を確認します。
# 曜日情報を追加(月曜:0, 火曜:1, 水曜:2, 木曜:3, 金曜:4、土曜:5、日曜:6)
df['weekday'] = df['Date'].dt.weekday
df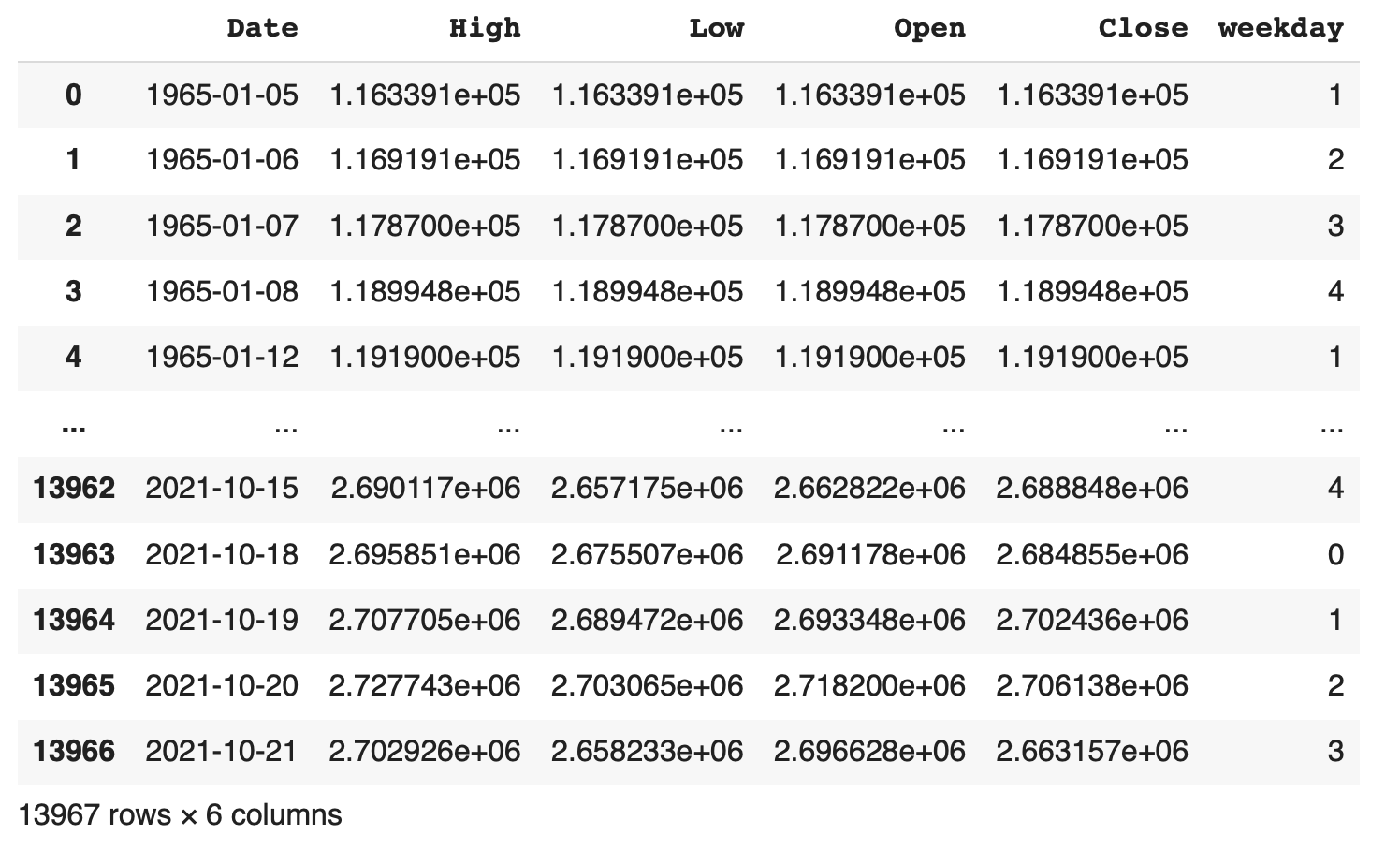
'weekday'のカラムが追加され0から4の数字が入力されている事がわかります。
また、株取引の行われない土曜日:5と日曜日:6のデータは存在していない事もわかります。
次に、1965年1月5日の週を基準に何周目となるのかの情報を追加します。
1965年1月5日が火曜日である事がわかるので、その週の頭の月曜日となる1965年1月4日を基準として、何日目となるのかの情報を追加します。
datetimeのライブラリからdatetimeとtimedeltaをインポートします。
基準となる日の1965年1月4日をdatetime関数を使って、変数startに代入します。
dfの'Date'カラムから基準のstartと引き算をすることで、何日目となるのかを計算します。これをtimedelta関数を用いて1週間となる7日周期で割ることで何週目かを計算する事ができます。
timedelta(weeks=1)と設定することで1週間となります。
この計算結果を'weeks'というカラムをdfに追加します。実行することで初めの週は0から始まり最後の2021年10月18日の週は2963となっている事が分かります。
# 初めの月曜日となる1965/1/4を基準に日数を追加
from datetime import datetime
from datetime import timedelta
start = datetime(1965,1,4)
df['weeks'] = (df['Date'] - start) // timedelta(weeks=1)
df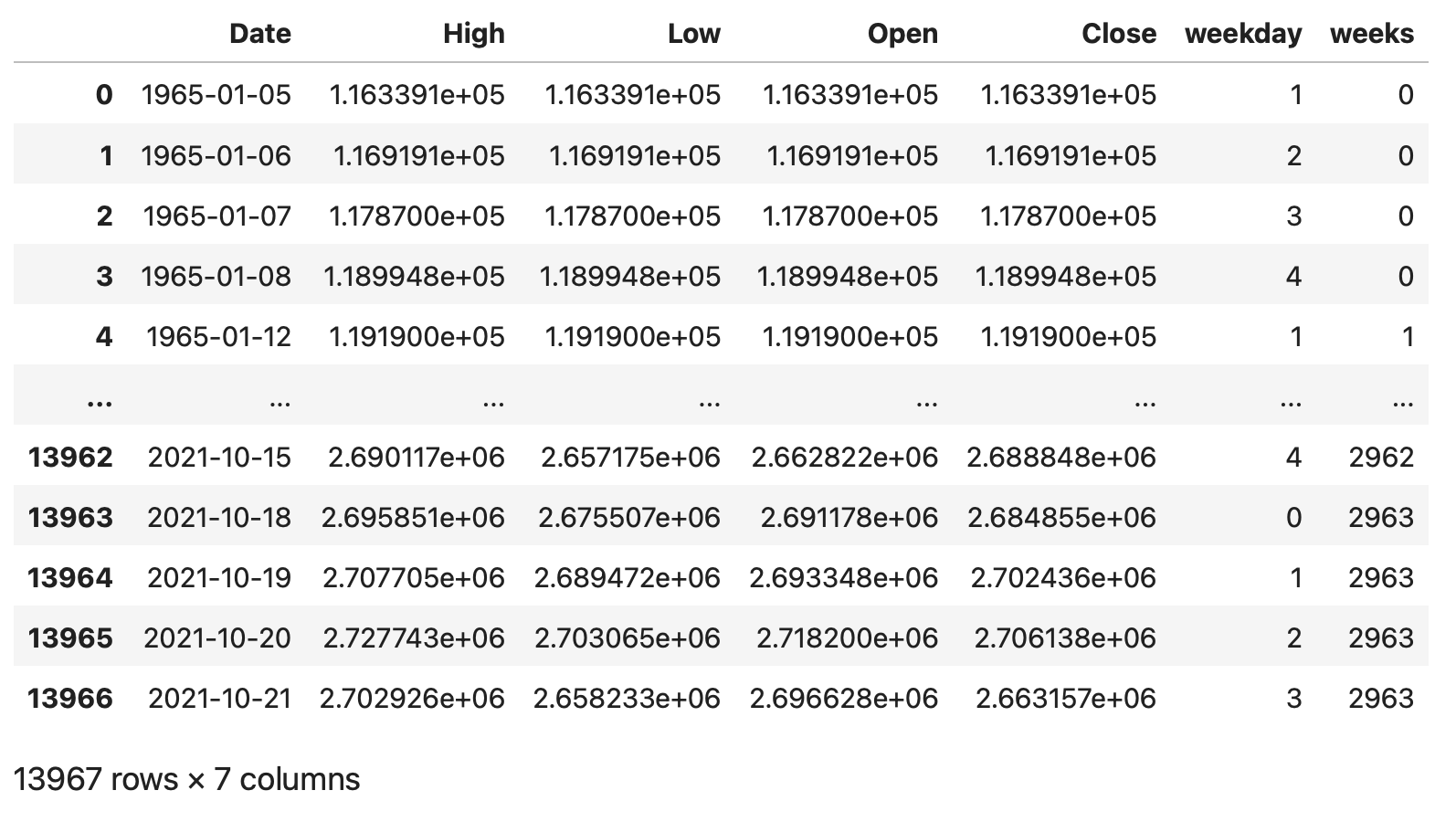
日付の情報の'Date','weekday','weeks'のカラムが分かれて表示されているので、見栄えを整理する目的で、一旦カラムの並び替えを行います。
先頭に日付の情報をまとめます。
並び替えたい順序でカラムを記述しdfを置き換えます。
実行する事で、並び替えられている事がわかります。
# カラムの並べ替え
df = df[['Date', 'weeks', 'weekday', 'High', 'Low', 'Open', 'Close']]
df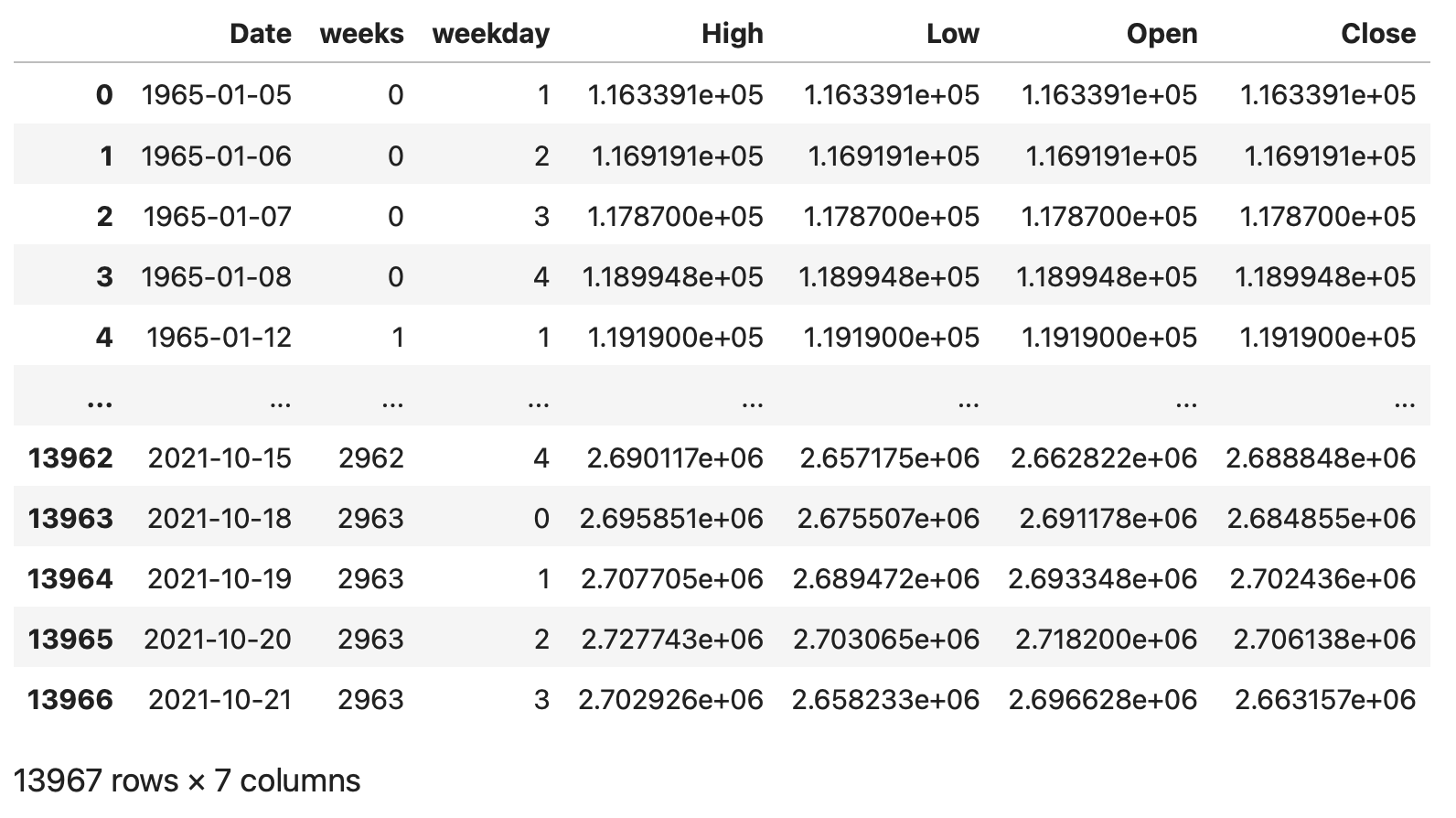
今回のような時系列データを処理する際には、set_indexメソッドを使ってindexを日付に設定します。念のためにsort_valuesメソッドを使って日付順に並び替えを行います。実行する事で、日付の'Date'がindexに設定されている事がわかります。
# データの並び替え
df.sort_values(by='Date', ascending=True, inplace=True)
# 日付をインデックスにセット
df.set_index(keys='Date', inplace=True)
df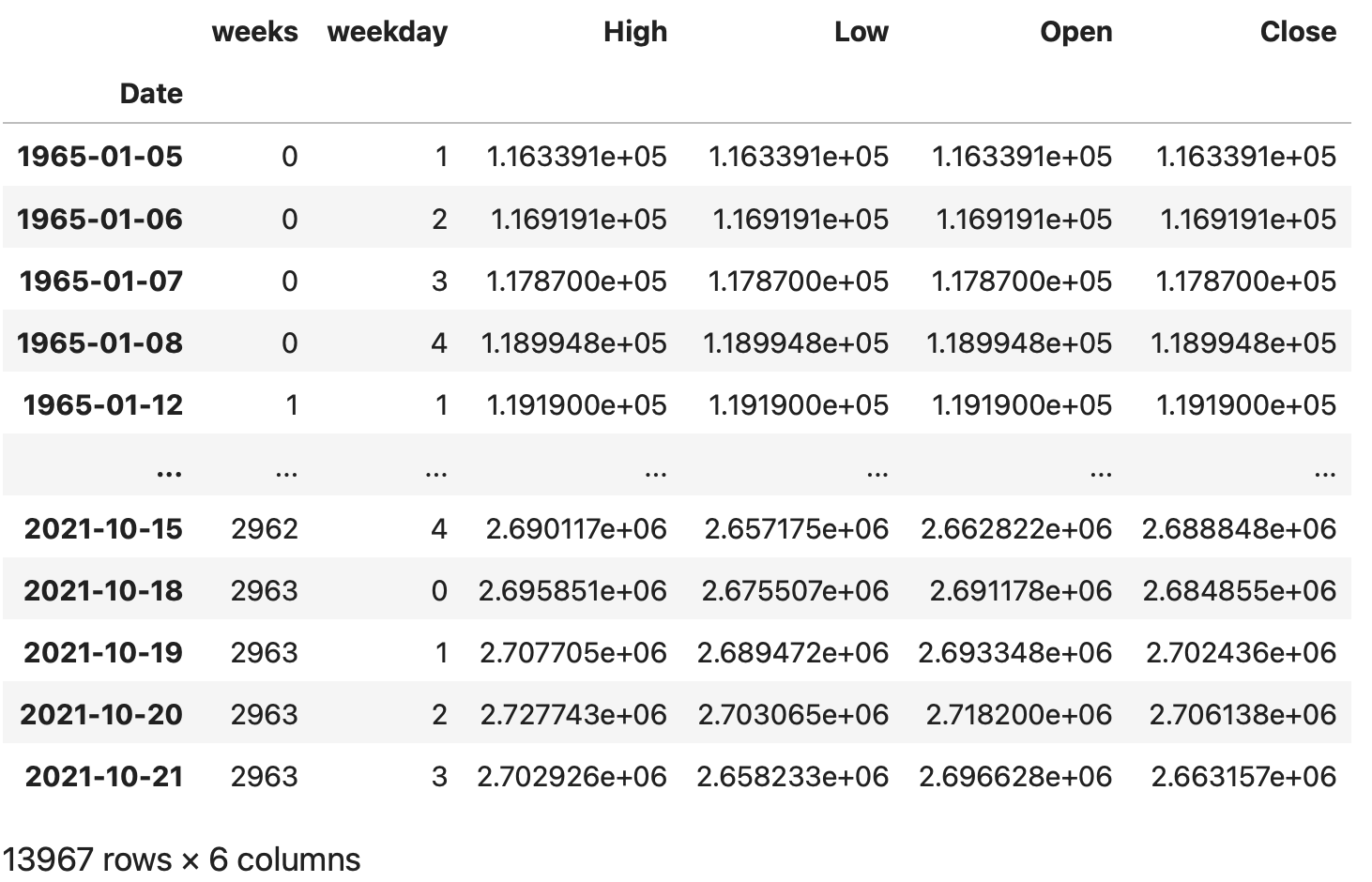
次に今回予測したい翌日の終値が本日の終値よりも上がるのかどうかの情報を追加します。shiftメソッドを用いてカラムの情報をずらすdfを作成する事ができるので、それを用いて計算を行います。
shift(-1)とする事で、カラムの情報を1行上にずらしたデータフレームを作成する事ができます。
dfを1行分上にずらしたものをdf_shiftとして作成します。実行する事でカラムの情報が1行分上にシフトしている事がわかります。一番下のカラムは欠損値となります。
#カラム情報を1行上にずらしたデータフレームを作成する
df_shift = df.shift(-1)
df_shift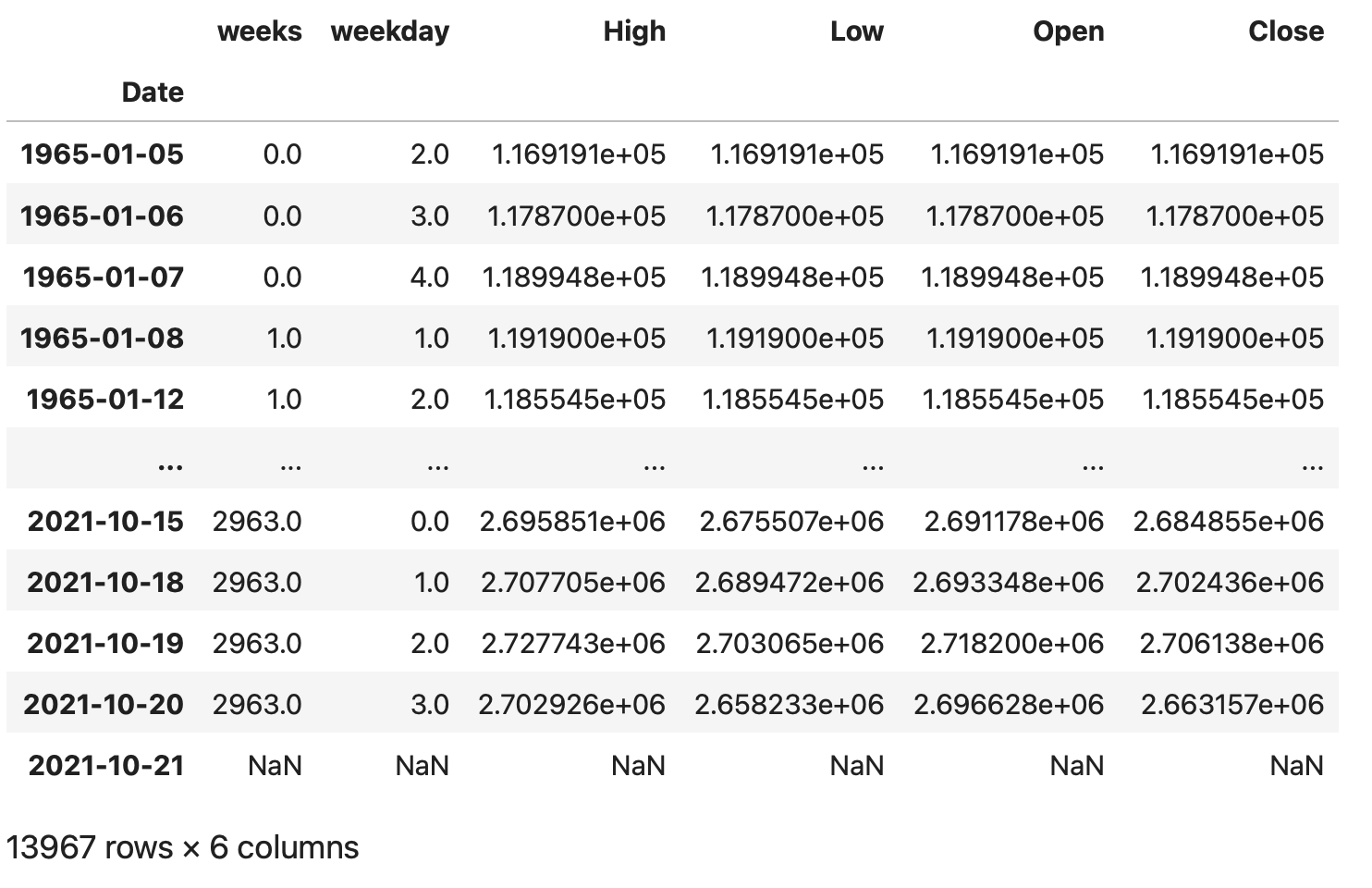
このdf_shiftを用いて、翌日の終値と本日の終値を引き算し、その結果を'delta_Close'というカラムを追加しdfに入力します。
#翌日の始値と本日の終値の差分を追加する
df['delta_Close'] = df_shift['Close'] - df['Close']
df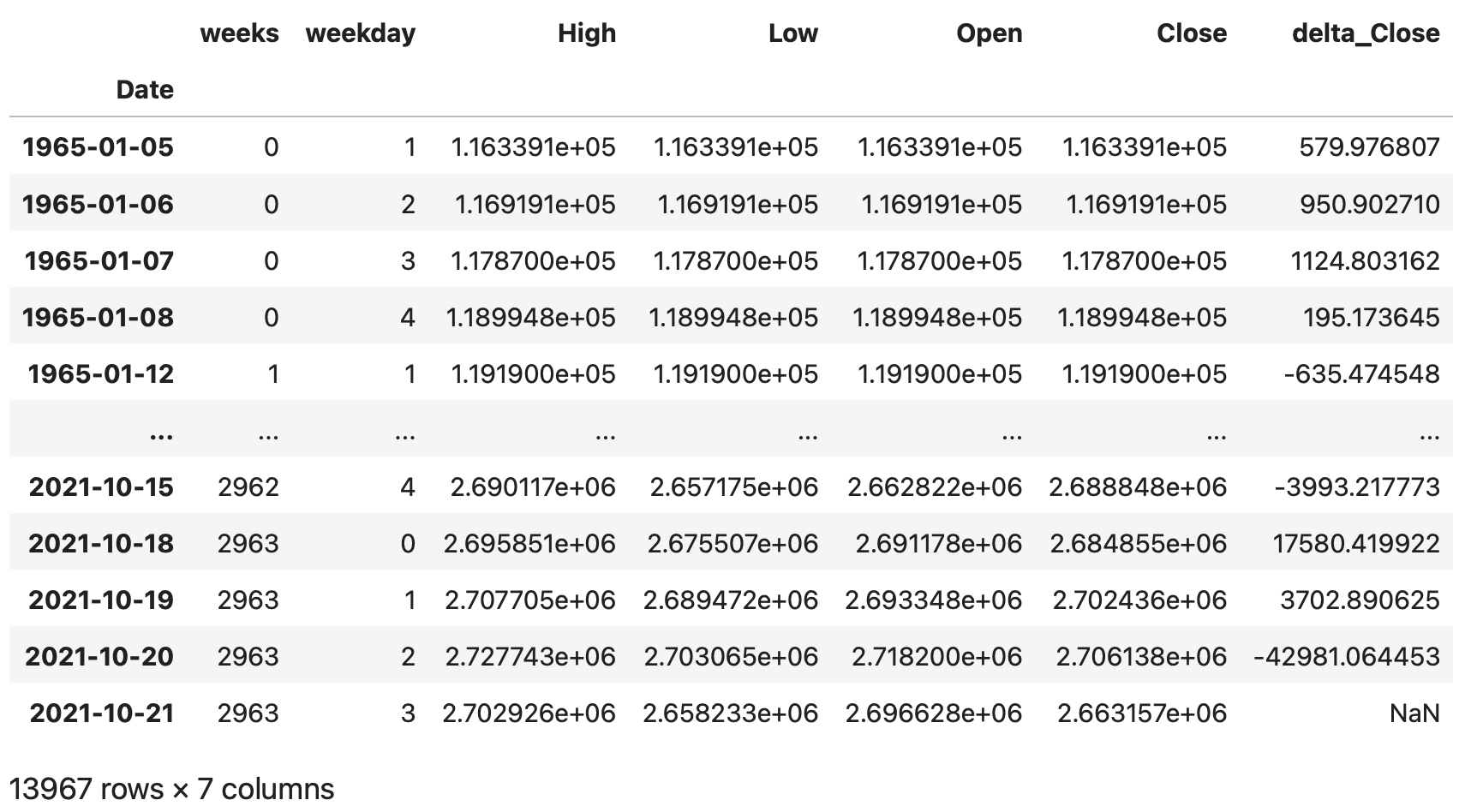
この'delta_Close'が上がる場合1、それ以外を0として目的変数となる'Up'のカラムを追加します。同時に'delta_Close'カラムの削除も行います。
#目的変数Upを追加する(翌日の終値が上がる場合1、それ以外は0とする)、'delta_Close'カラムの削除
df['Up'] = 0
df['Up'][df['delta_Close'] > 0] = 1
df = df.drop('delta_Close', axis=1)
df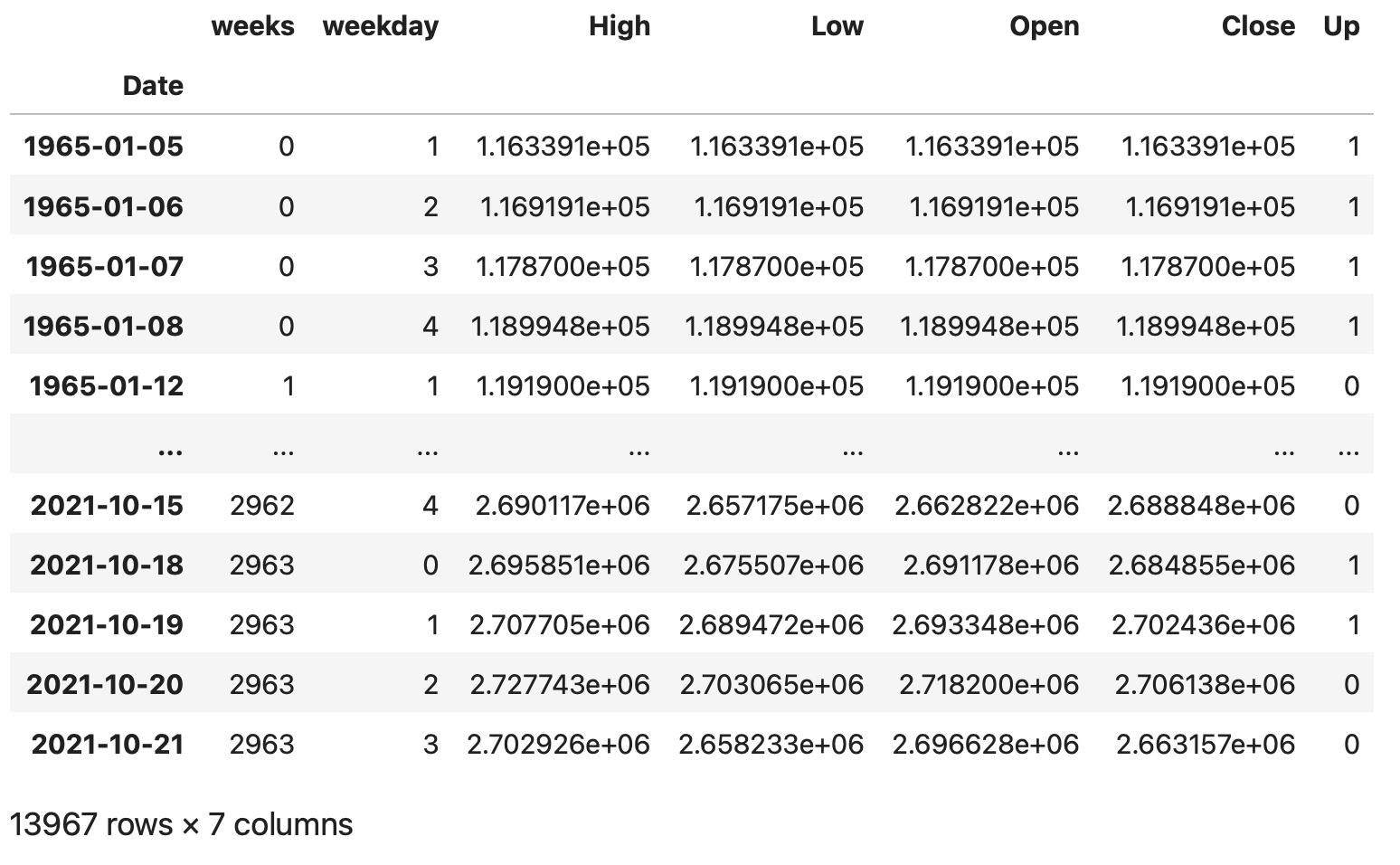
ここまでで、下準備となる週番号、曜日、目的変数の追加が終わりました。
データの全体像をつかむ
時系列データをグラフで表示する事で、株価変動の大まかなイメージを掴みます。
'Open', 'High', 'Low', 'Close'を抜き出しdf_newを作成後に、pyplotを用いてグラフ化行います。
matplotlibのライブラリからpyplotをpltという名前でインポートします。
df_newにplotメソッドを用いて、引数'kind=line'とする事で折れ線グラフが作成されます。pyplotのshowメソッドでグラフを表示します。
初めの1965年から1990年頃までは、上昇傾向となっています。その後は下がる傾向となり、2010頃より再度上昇傾向である事がわかります。
# 'Open', 'High', 'Low', 'Close'グラフ化のためにカラム抽出
df_new = df[['Open', 'High', 'Low', 'Close']]
# matplotlibのインポート
from matplotlib import pyplot as plt
# 時系列折れ線グラフの作成
df_new.plot(kind='line')
plt.show()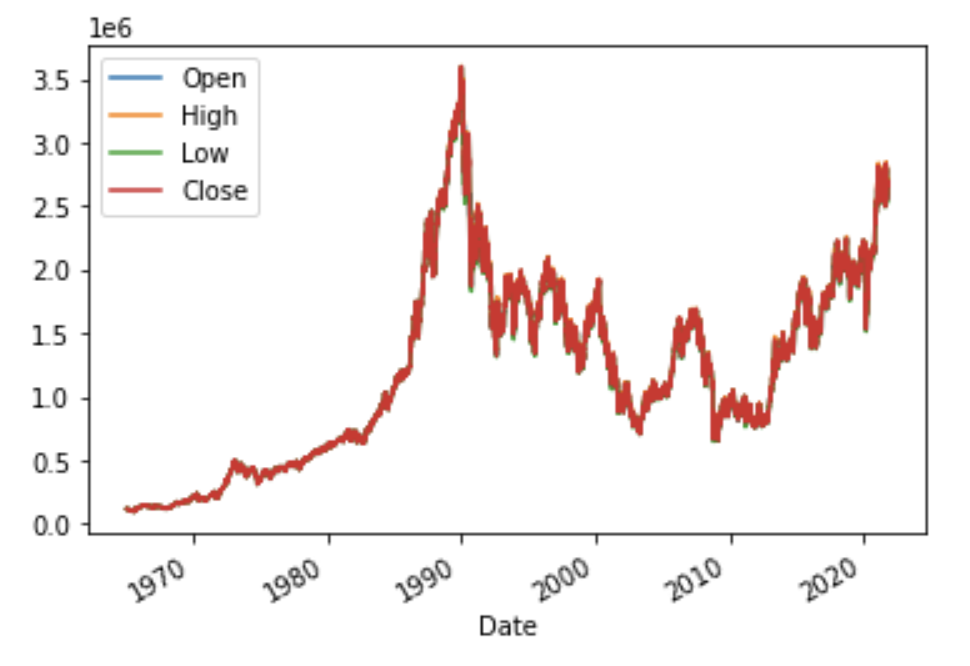
特徴量を追加する
予測を正しく行えるようにする為の情報量(特徴量)を追加します。現在dfに入っている始値、終値、最高値、最安値の情報だけを用いて予測する事も可能ですが、株価の変動に影響すると言われている一般的な情報を追加していきます。
終値の前日比率と、始値と終値の差分カラムに追加します。
まず終値の前日比率ですが、本日の終値が前日から何%変動したのかを表す値となります。
(今日の終値 - 前日の終値) ÷ 前日の終値
で計算します。
shiftメソッドを用いて、今度は1行したにずらしたデータフレームを作成し、終値の前日比率'Close_ratio'を計算しdfにカラムを追加します。
# 終値の前日比の追加
df_shift = df.shift(1)
df['Close_ratio'] = (df['Close'] - df_shift['Close']) / df_shift['Close']
df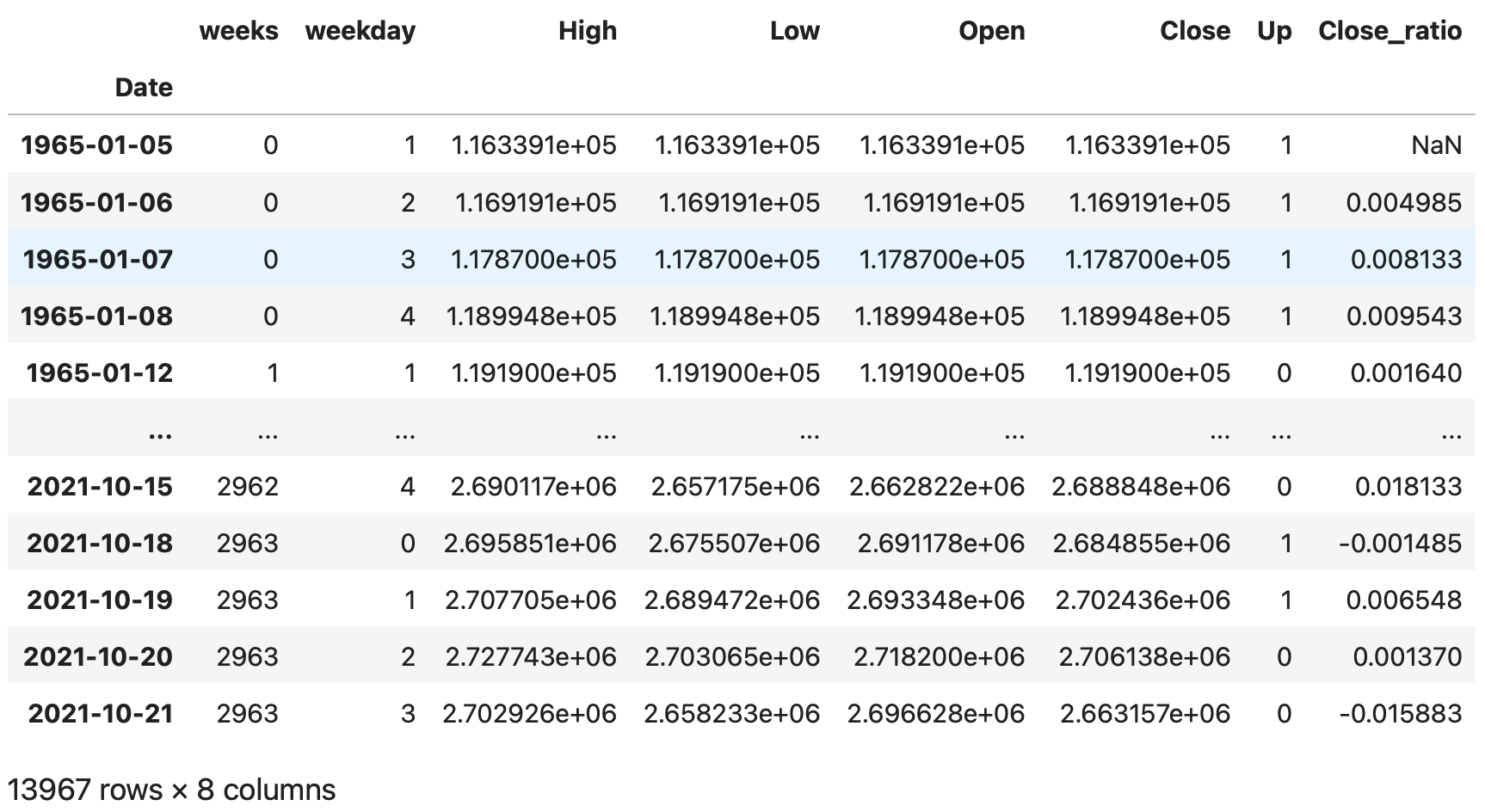
次に、始値と終値の差分'Body'をdfに追加します。
# 始値と終値の差分を追加
df['Body'] = df['Open'] - df['Close']
df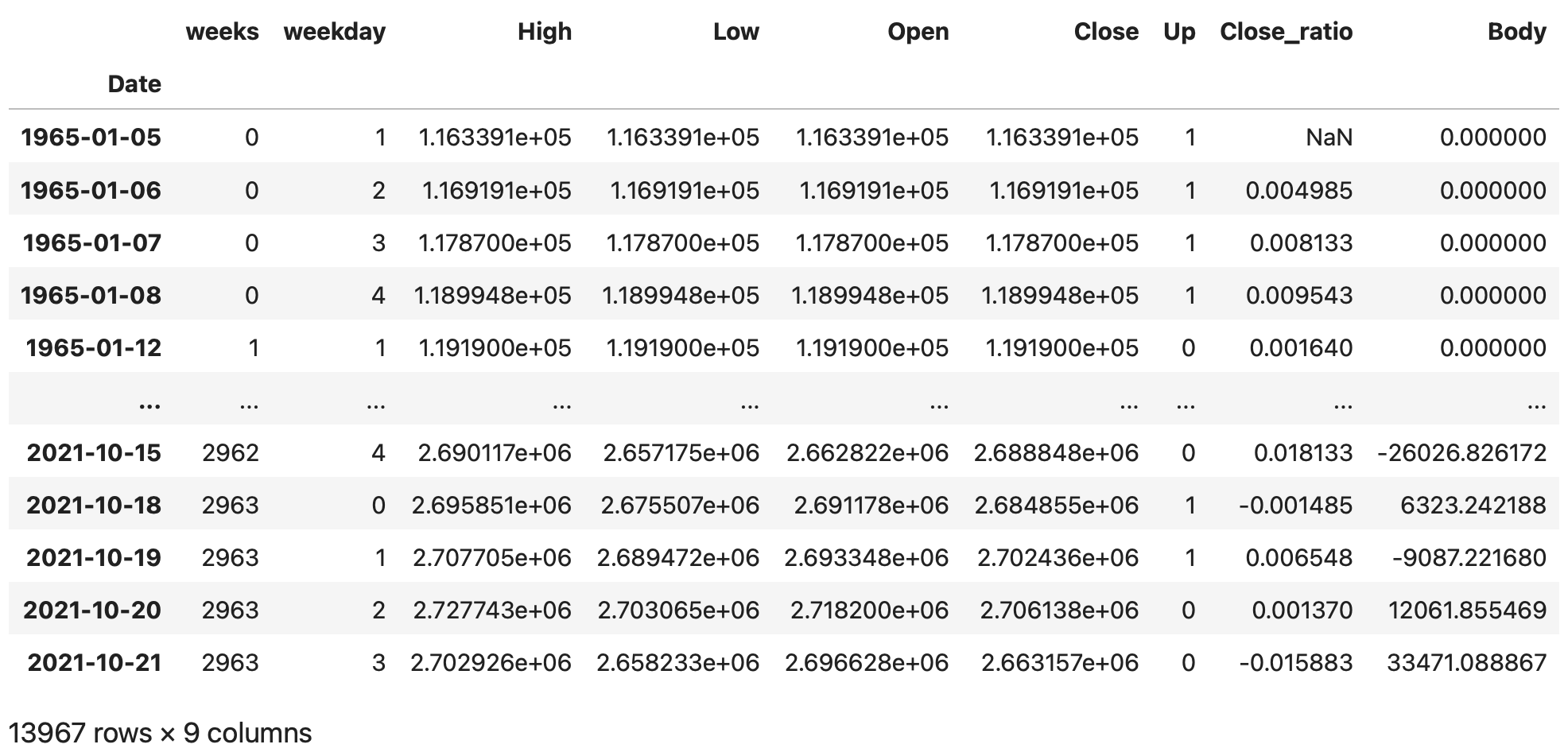
特徴量の追加は以上になります。次に、不要なデータの削除を行います。今回、月曜日から木曜日までの情報を用いて、金曜日の始値が上がるか下がるのかを予測するモデルを作成するために、各週で月曜日から金曜日までのデータが揃っている週だけ使用します。祝日や年末年始など株取引が行われていない日はデータがない為、5日分のデータが揃っていない週が存在しています。
各週毎に何日分のデータが存在しているのかを調べて、5日分揃っている週のデータを持ってきます。
手順としては、週番号'weeks'のリストを作成します。その後リストから取り出した同じ週番号のデータ数をカウントして行き結果をdfに格納し、5日揃っている週だけ残す処理をします。
週番号は0から2963まで連番で有ると考えられ、0から順番に処理すれば良いと考えられますが、万が一抜けている週が存在して居ても処理が行えるように、あえて週番号を抜き出したリスト(list_weeks)を作成します。
# 週番号をリストに格納
list_weeks = []
list_weeks = df['weeks'].unique()
list_weeks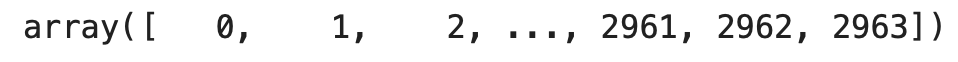
リストに従い、for文を用いて、週毎の日数をカウントしたカラム'week_days'にカウント数を入力します。
# 各週ごとの日数を入力
df['week_days'] = 0
for i in list_weeks:
df['week_days'][df['weeks'] == i] = len(df[df['weeks'] == i])
df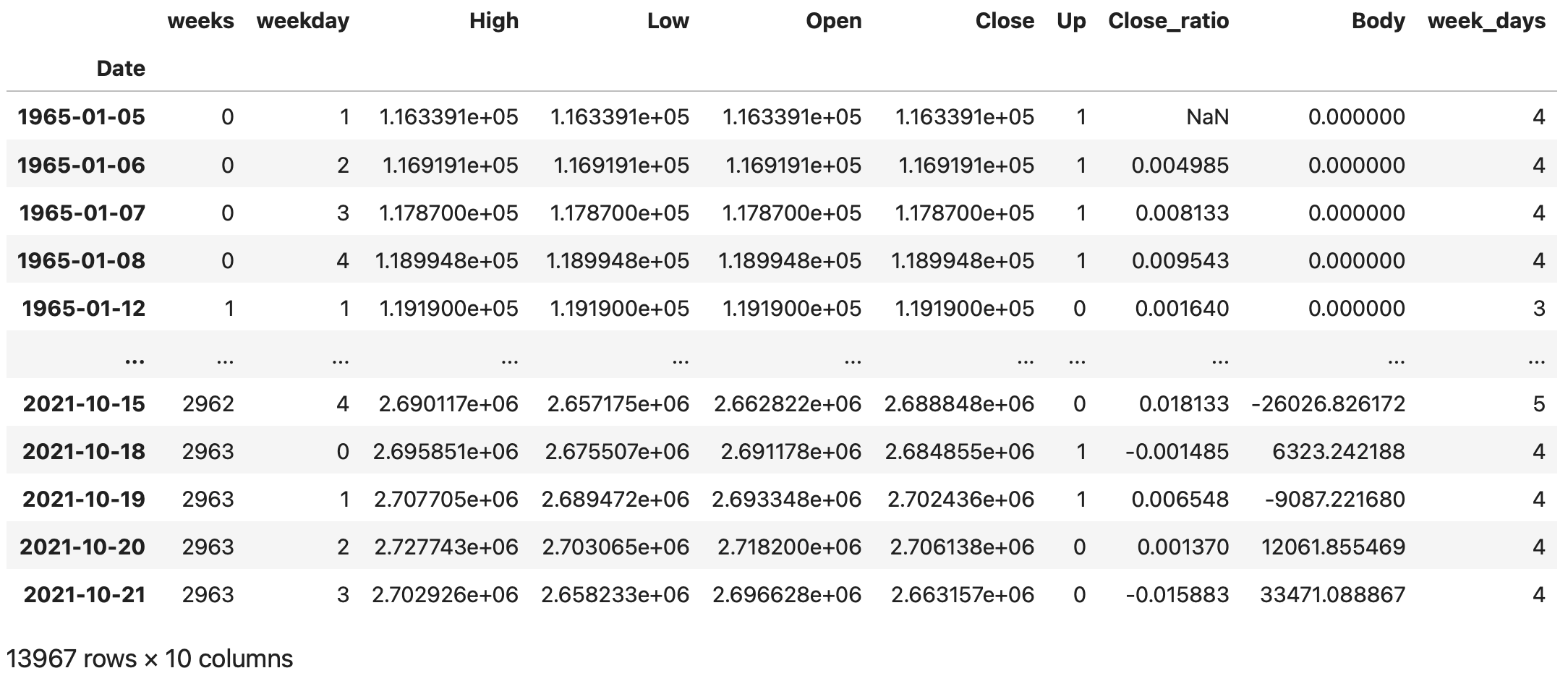
5日データの存在する週(week_daysが5)の週のデータを抜き出して、dfに入力します。
# 月曜〜金曜まで5日分データのある週だけデータを取り出す
df = df[df['week_days'] == 5]
df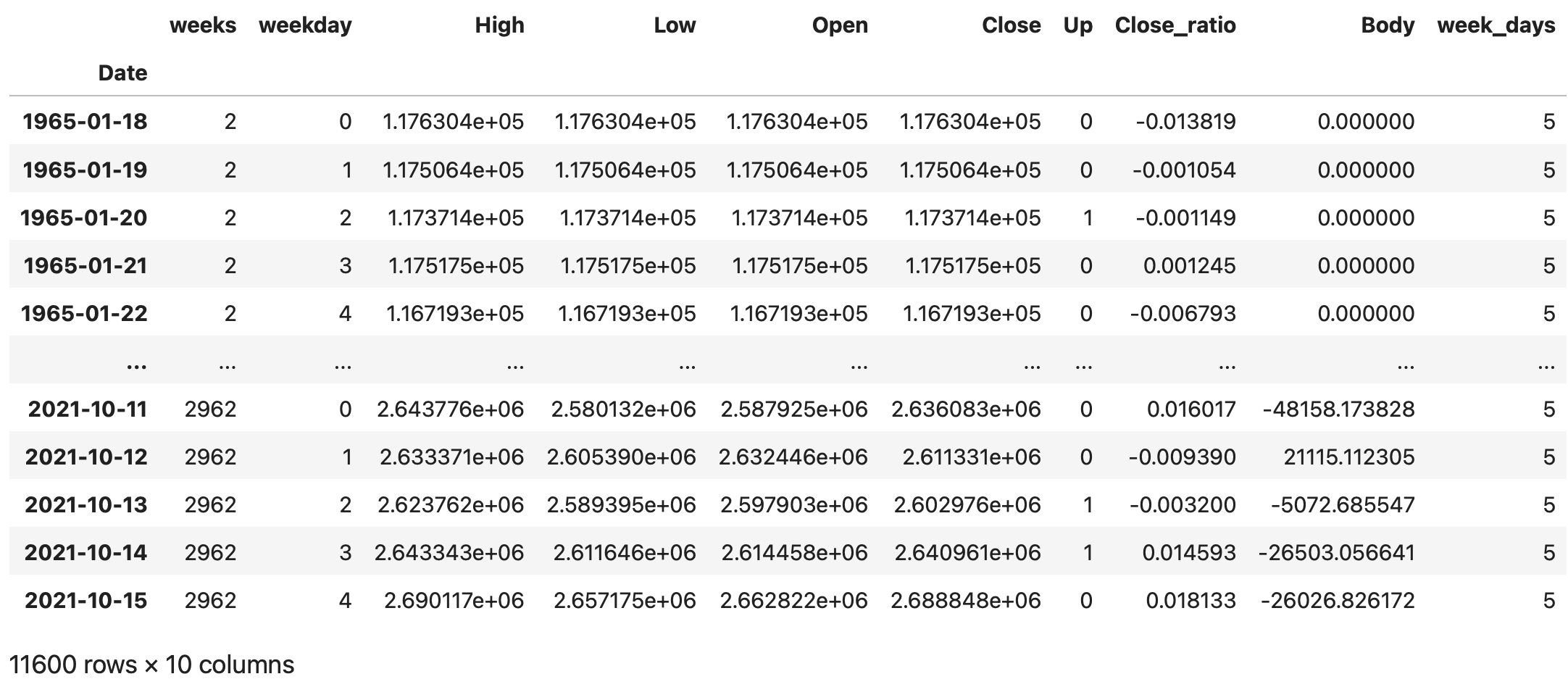
予測に使用しない金曜日のデータ(weekdayが4)を削除します。
_
#金曜日のデータを削除する(weekday:4となるデータ)
df = df[df['weekday'] != 4]
df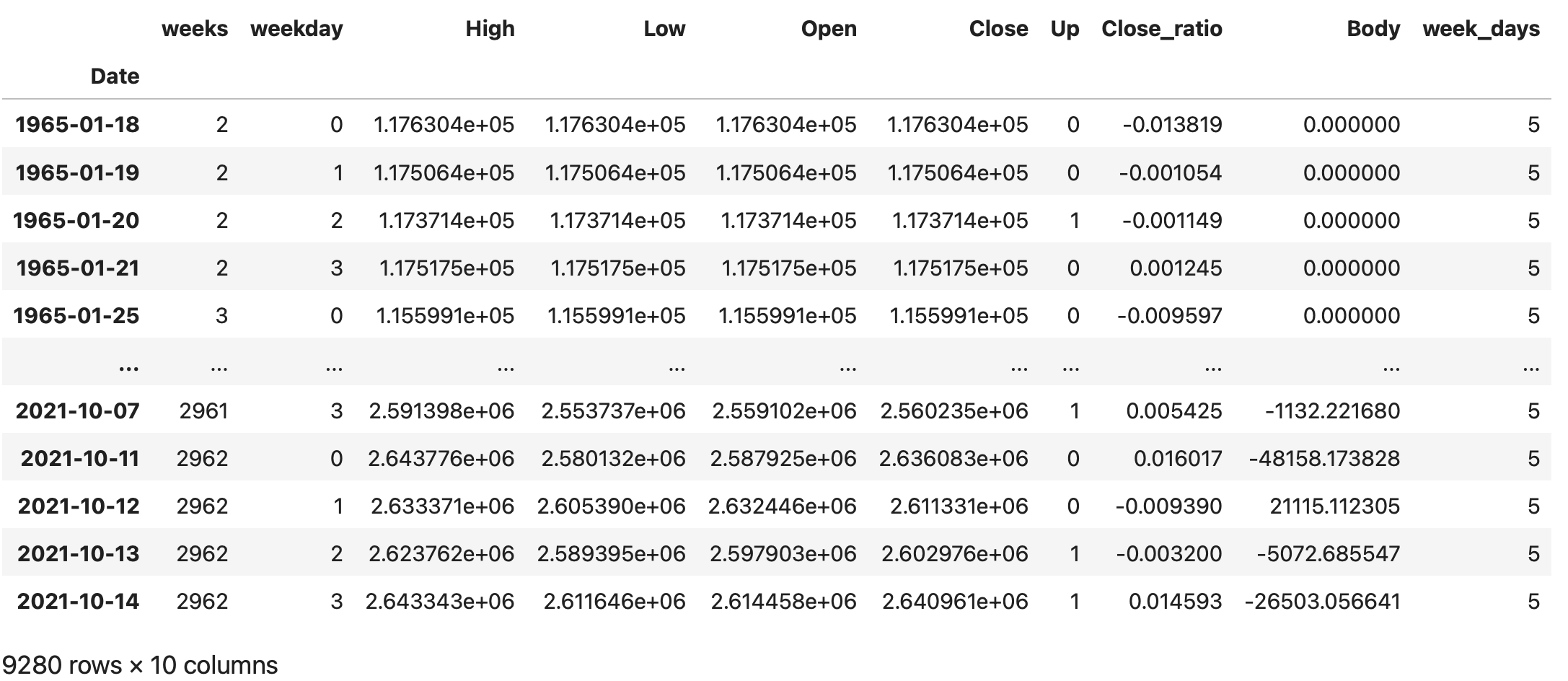
不要カラムの削除と並び替えを行います。
# 不要カラムの削除と並べ替え
df = df[['weekday', 'High', 'Low', 'Open', 'Close', 'Close_ratio', 'Body', 'Up']]
df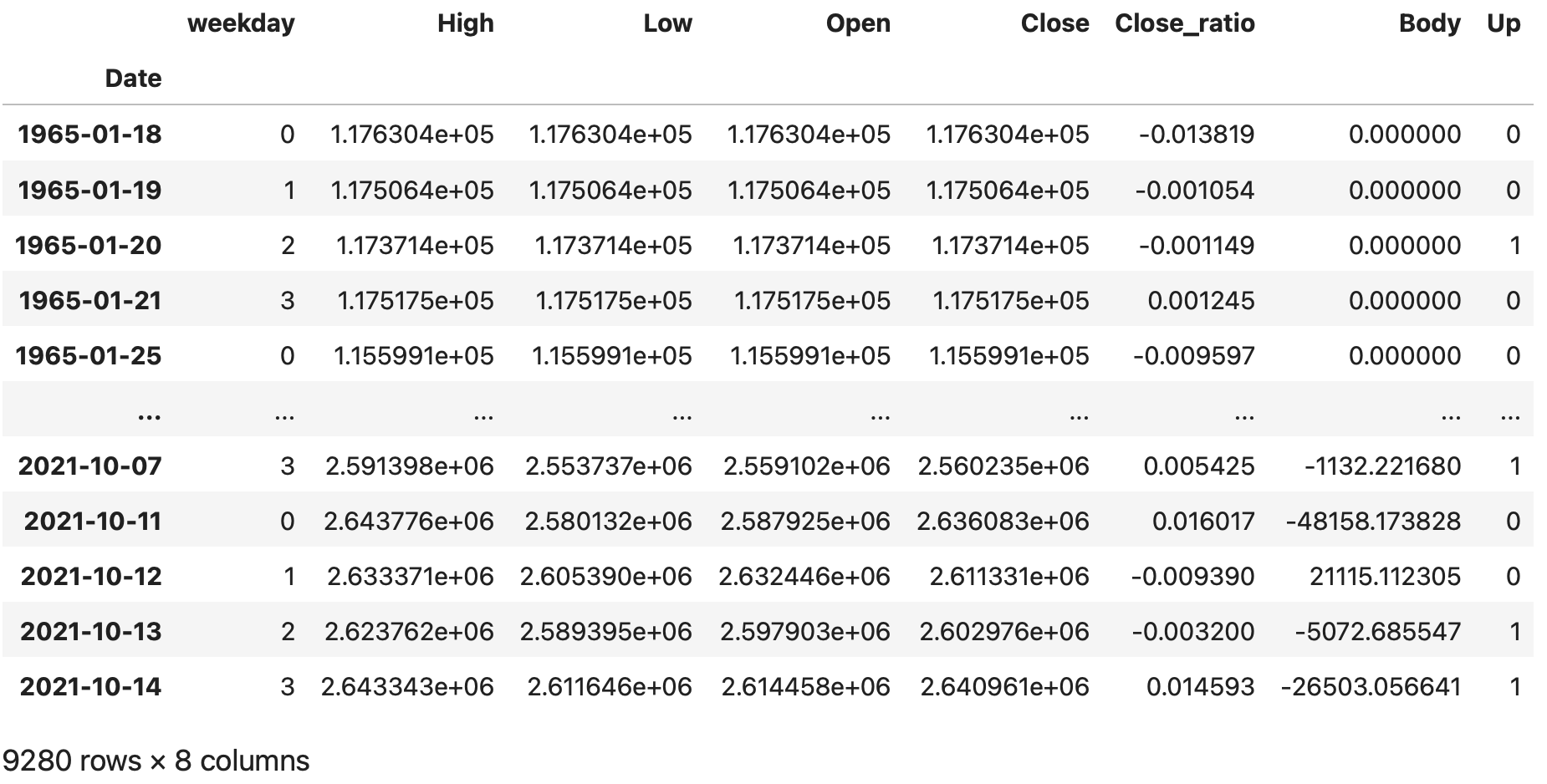
ここまでで、データの準備は完了です。
学習データと検証データに分割する
さて、ここからは直近の2018年以降のデータを使用します。
2018年から2020年を学習データ、2021年以降を検証データとして分割します。
datetime64型をindexに設定している時系列のデータフレームは、期間を設定してデータを抜き出す事ができます。
2018年1月1日から2020年12月31日までのデータを抜き出し、df_trainに入力します。
# 学習データを2018-01-01〜2020-12-31の期間としdf_trainに入力する
df_train = df['2018-01-01' : '2020-12-31']
df_train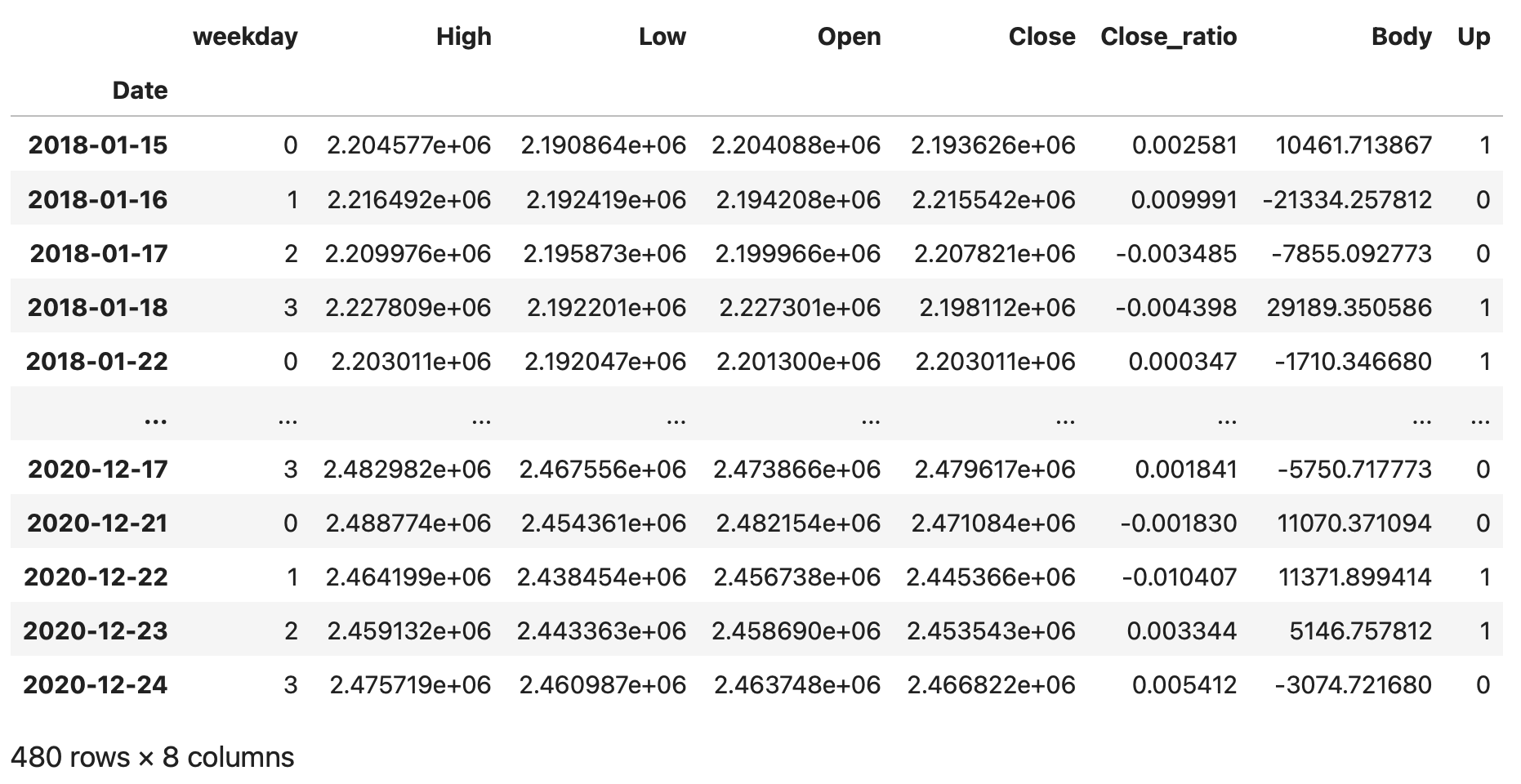
同様に、2021年1月1日以降のデータを抜き出し、df_valに入力します。
# 検証データを2021-01-01以降としてとしてdf_valに入力する
df_val = df['2021-01-01' : ]
df_val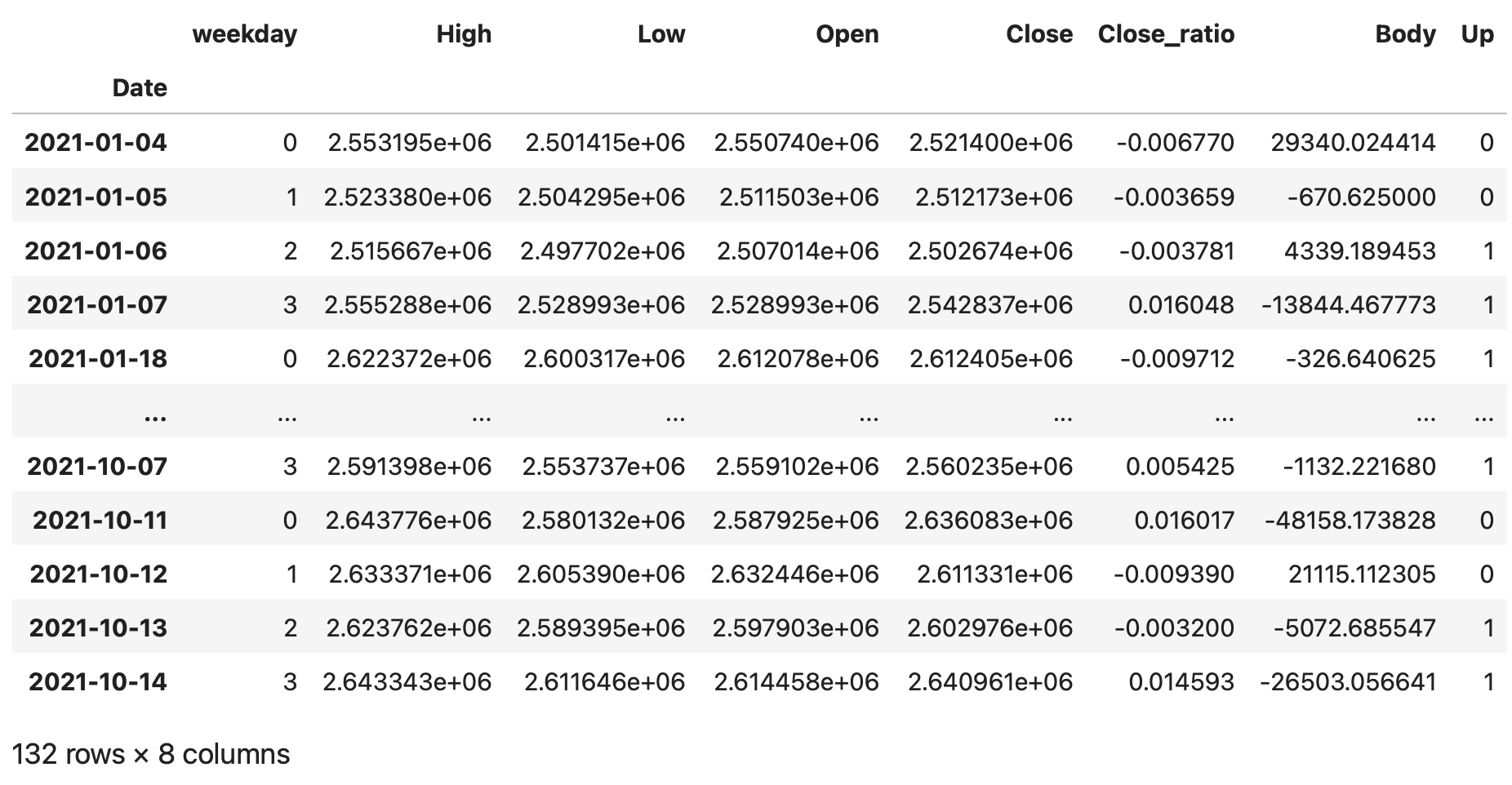
学習データと検証データをそれぞれ、説明変数と目的変数に分けます。
説明変数のカラムは'weekday', 'High', 'Low', 'Open', 'Close', 'Close_ratio', 'Body'を
目的変数のカラムは'Up'になります。
学習データの説明変数をX_train、学習データの目的変数をy_trainとしてカラムを指定して、それぞれを入力します。また、表示することでX_train, y_trainそれぞれに指定した期間内のデータが入力されていることが分かります。
# 学習データを説明変数(X_train)と目的変数(y_train)に分ける
X_train = df_train[['weekday', 'High', 'Low', 'Open', 'Close', 'Close_ratio', 'Body']]
y_train = df_train['Up']
# 学習データの説明変数と目的変数を確認
print(X_train)
print(y_train)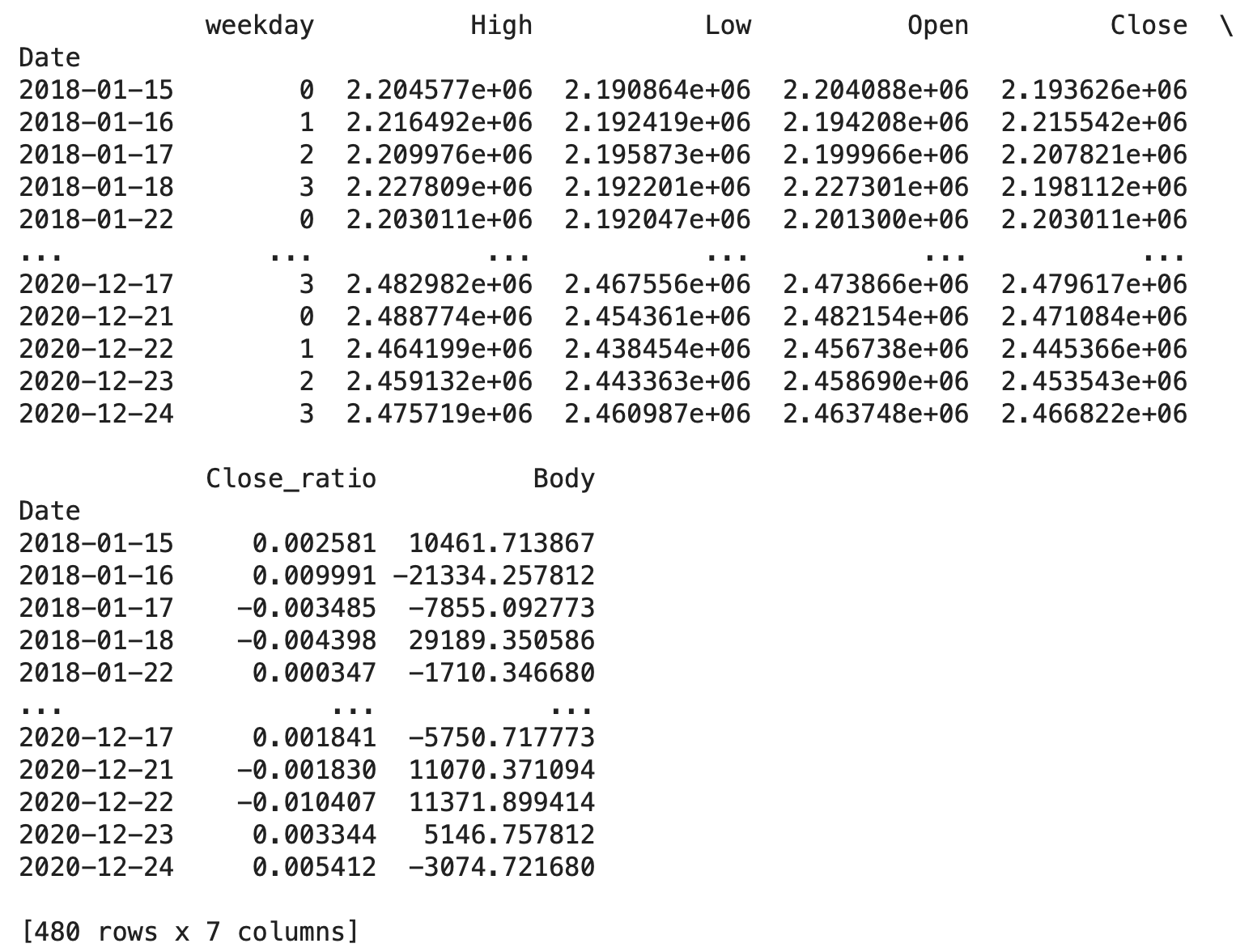
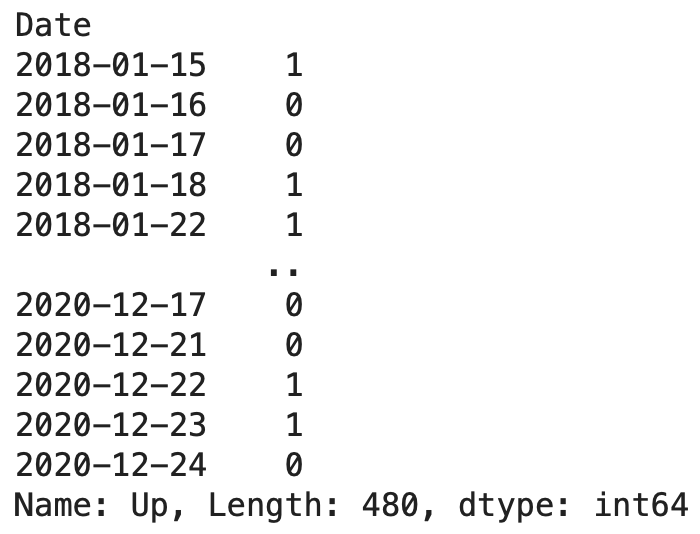
同様に検証データの説明変数をX_val、目的変数をy_valとしてデータを入力し、確認します。
# 検証データを説明変数(X_val)と目的変数(y_val)に分ける
X_val = df_val[['weekday', 'High', 'Low', 'Open', 'Close', 'Close_ratio', 'Body']]
y_val = df_val['Up']
# 検証データの説明変数と目的変数を確認
print(X_val)
print(y_val)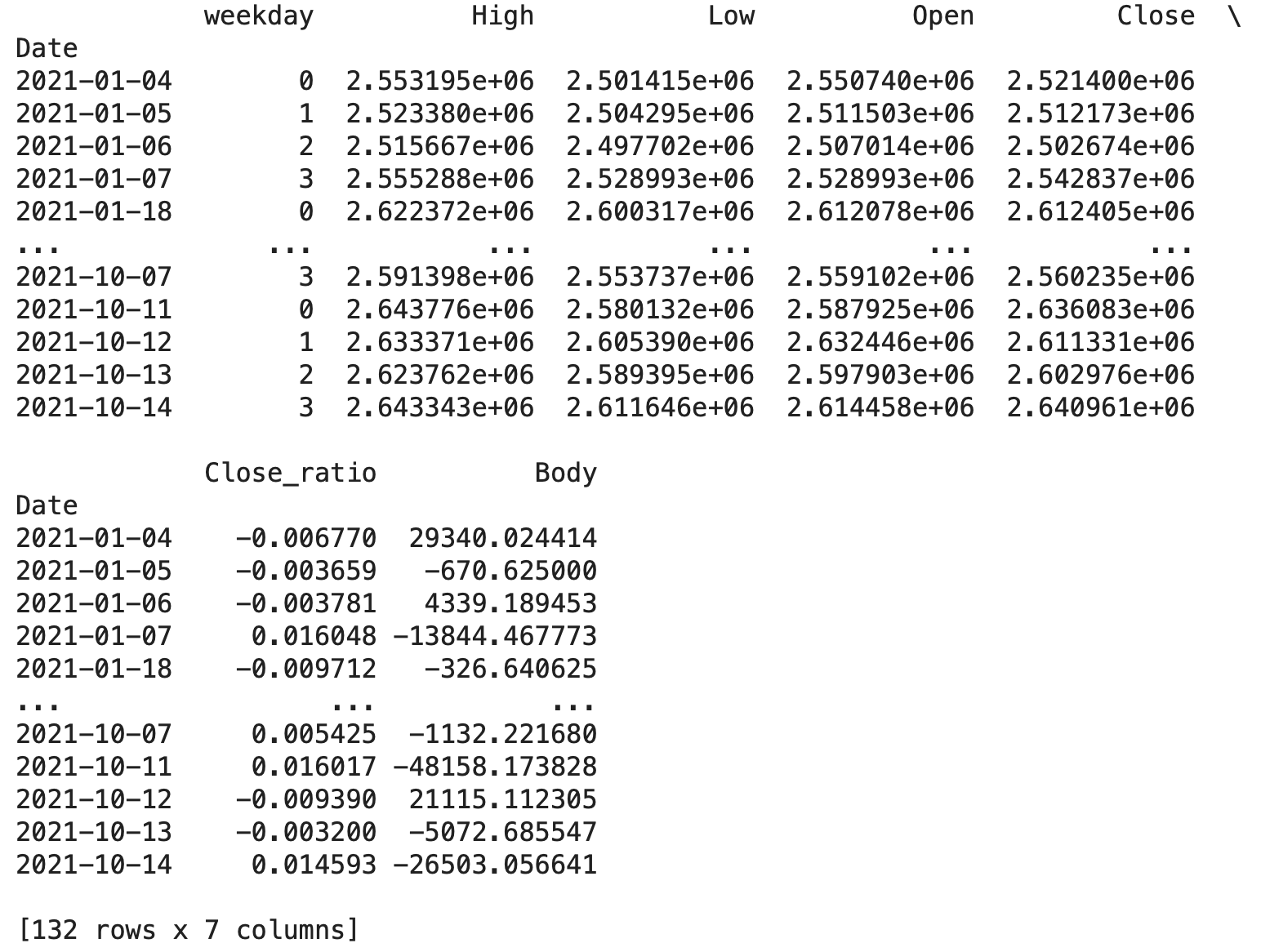
学習データと検証データの時系列グラフを作成し2021年前後でデータが分かれていることを目で確認します。2021年以前が学習データで青いグラフ、2021年以降が検証データでオレンジのグラフで示されている事が分かります。
# 学習データと検証データの終値(Close)の折れ線グラフ作成
X_train['Close'].plot(kind='line')
X_val['Close'].plot(kind='line')
# グラフの凡例を設定
plt.legend(['X_train', 'X_val'])
# グラフの表示
plt.show()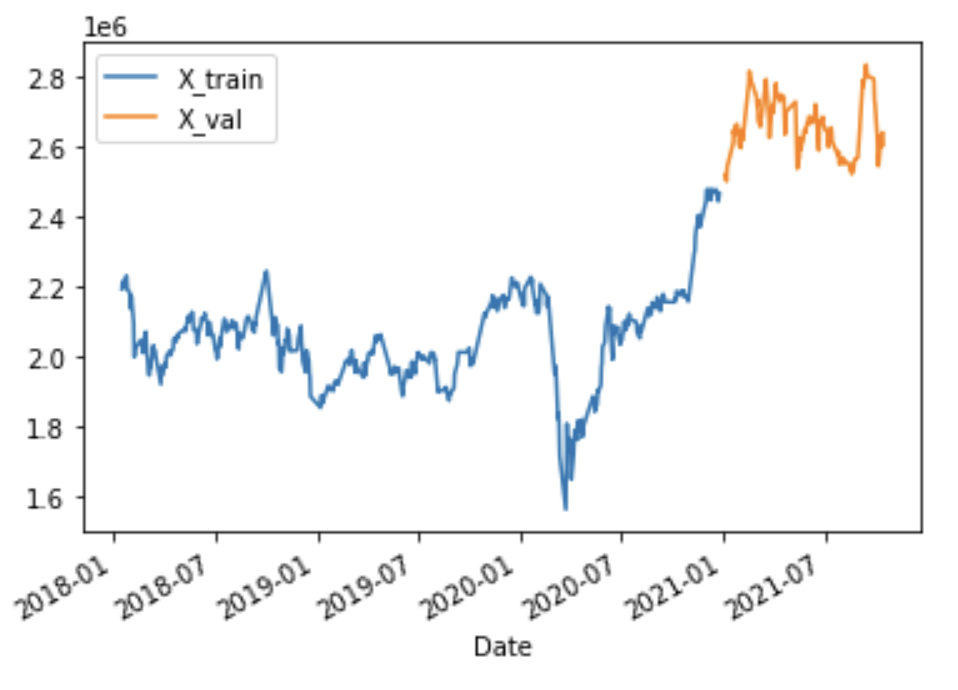
データを整える
予測モデルに学習をさせるために、データを整えます。
説明変数は各週毎の月曜日から木曜日の4日間をセットとして一つにまとめます。また、目的変数は翌日の金曜日の始値が上がるか下がるかを示す木曜日のデータを抜き出します。機械学習を行うためには説明変数と目的変数の数を揃える必要があります。
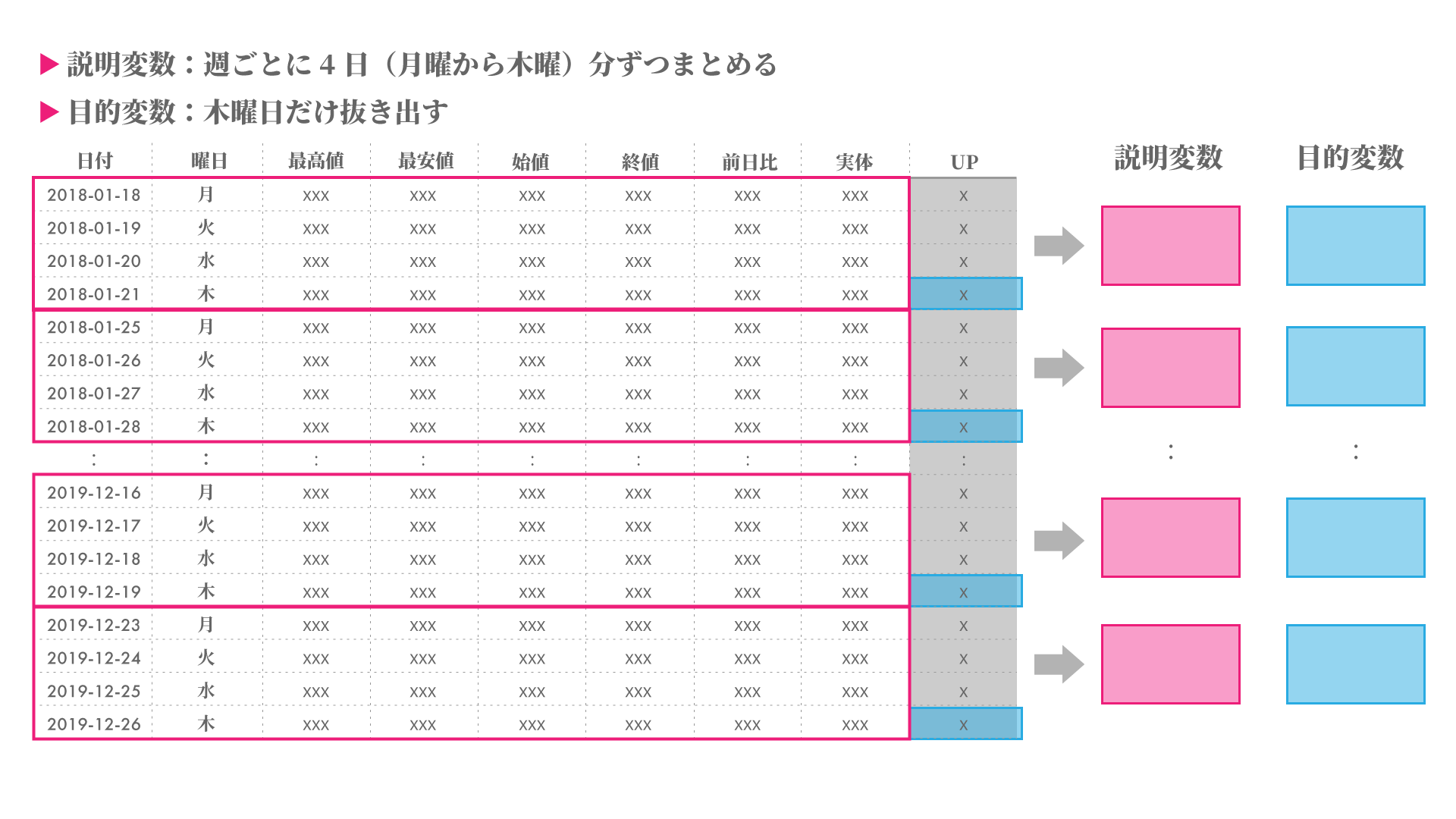
説明変数を抜き出す期間により、株価の金額や変動量が違っています。
例えば、2020年4月頃は株価が16000円程度であったのに対し、12月頃には25000円を超えていたり、同じ週でも株価の変動が大きい事もあります。
このように抜き出している期間内において、データの大きさや変動幅が大きく異なっている場合、機械学習では予測が正しく行えない事があります。このような場合に標準化という処理を行うことが有ります。
この処理を行うことで、平均が0で±3以内の範囲に収める事が出来るために、機械は計算の処理がし易くなり、また予測精度が向上する事もあります。
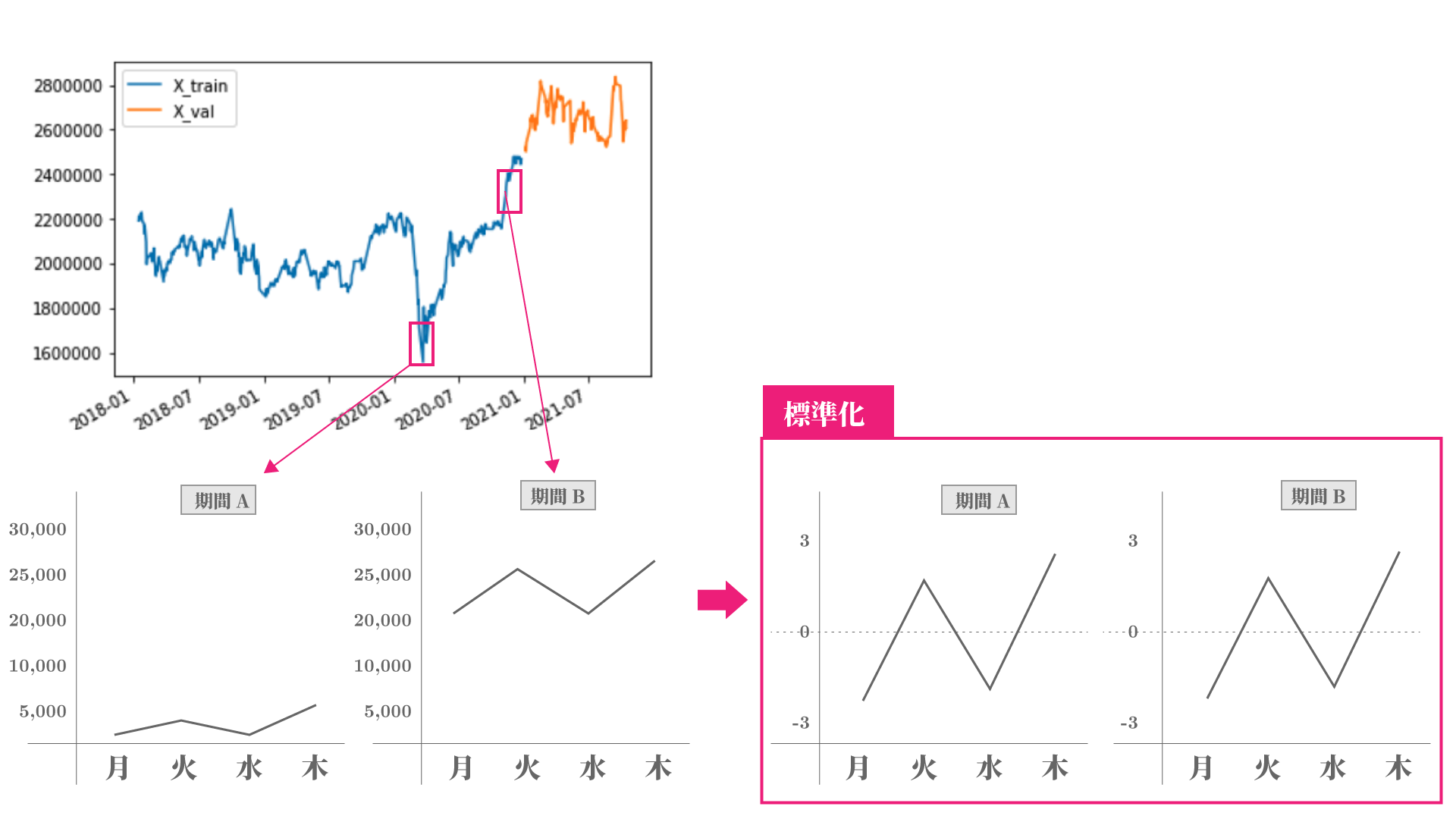
この4日毎にデータを抜き出して、標準化を行うための処理を、sklearnのpreprocessingというライブラリのStandardScalerという関数を使って、for文の繰り返し処理を用いて次のような関数を定義します。
また今回、機械学習に使用する予測モデルはLSTMというニューラルネットのモデルを使用します。このモデルではnumpy配列という形式のデータを用います。
# 標準化関数(StandardScaler)のインポート
from sklearn.preprocessing import StandardScaler
# numpyのインポート
import numpy as np
# 4日ごとにデータを抜き出して、標準化ととnumpy配列に変換する関数(std_to_np)の定義
def std_to_np(df):
df_list = []
df = np.array(df)
for i in range(0, len(df) - 3, 4):
df_s = df[i:i+4]
scl = StandardScaler()
df_std = scl.fit_transform(df_s)
df_list.append(df_std)
return np.array(df_list)標準化を行うStandardScalaerをsklearn.preprocessingから、numpyをnpとしてインポートします。次に4日毎にデータを抜き出し、標準化を行い、numpy配列で出力する関数(std_to_np)を定義します。
df_list = [] でまず空のリストを定義します。ここには標準化をおこなった後の、4日毎にまとまったデータを格納して行きます。
df = np.array(df) で入力されたデータフレームをまずnumpy配列に変換します。
この配列に対して、for文を用いて4日ずつのデータ抜き出して、df_sに入力(df_s = df[i:i+4])した後に、StandardScalerをインスタンス化し(scl = StandardScaler()) 標準化をおこなった結果をdf_stdに入力(df_std = scl.fit_transform(df_s))し、それをはじめに定義したdf_listにappendメソッドを用いて格納(df_list.append(df_std))して行きます。最後の4日分のデータまでこの繰り返し処理を行います。
繰り返し処理が終了すると、df_listをnumpy配列で出力(return np.array(df_list))します。
この関数をX_trainとX_valに適用してデータの型を確認します。
# 学習データと検証データの説明変数に関数(std_to_np)を実行
X_train_np_array = std_to_np(X_train)
X_val_np_array = std_to_np(X_val)
# 学習データと検証データの形の確認
print(X_train_np_array.shape)
print(X_val_np_array.shape)出力結果から、480日分あったX_trainが4分の1の120個のデータとなり、132日分あったX_valが4分の1の33個のデータになっている事がわかります。
それぞれの数に続く'4'は月曜から木曜の4日分のデータ数を表しており、'7'は説明変数('weekday', 'High', 'Low', 'Open', 'Close', 'Close_ratio', 'Body')のカラム数を表しています。
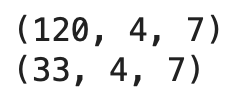
続いて、目的変数の木曜日のデータだけ抜き出します。抜き出す前に一旦、学習データと検証データのデータを確認します。
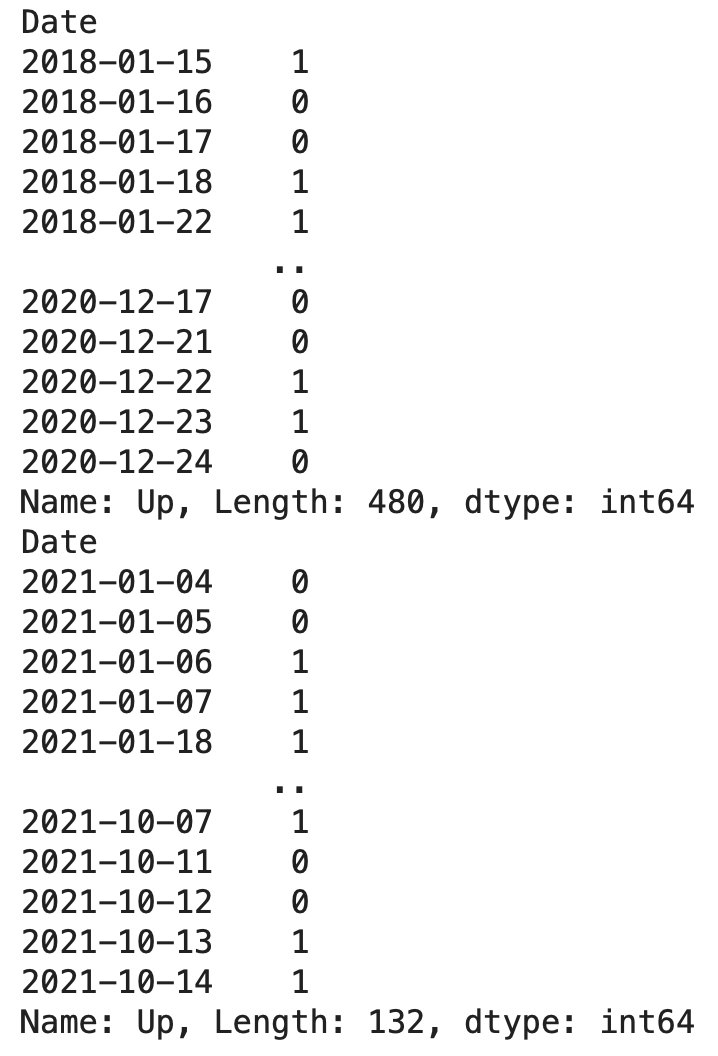
# 学習データと検証データの目的変数を確認
print(y_train)
print(y_val)学習データは480個、検証データは132個有ることがわかります。
これらのデータに対して、各週の4日目(木曜日)のデータを抜き出して確認します。
# 学習データ、検証データの目的変数の間引き
# 週の4日目(木曜日)のデータだけ抜き出す
y_train_new = y_train[3::4]
y_val_new = y_val[3::4]
# 間引き後の学習データと検証データの目的変数を確認
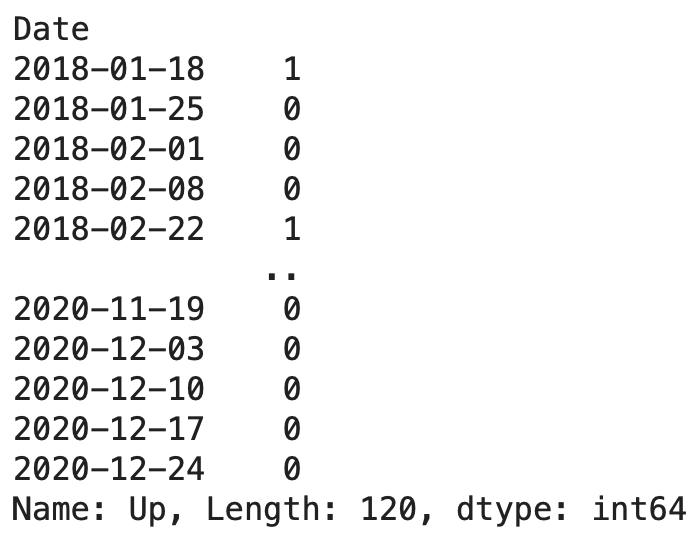
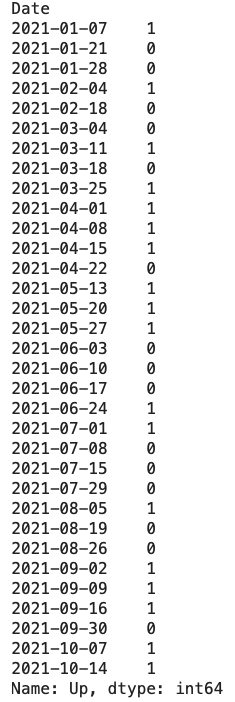
print(y_train_new)
print(y_val_new)学習データと検証データそれぞれ各週の4日目のデータのみになっており、個数は120個と33個となっており、4日毎にまとめた説明変数のデータ数と同じになっています。
これで、機械学習を行うためのデータは整いました。
予測モデルの作成
ニューラルネットの1種のLSTMを用いて予測モデルの作成と、検証データを用いた予測精度の検証をします。
LSTMを使用するためにkerasのライブラリを使えるようにする必要があります。まずこのためにtensorflowをインストールします。個人の環境で、インストール済みの方は不要ですが、google colabolatoryを使用の方は毎回行う必要があります。インストールは次のコマンドで数秒で完了します。
!pip install tensorflow続いて、kerasから必要な関数をインポートします。
# keras.modelsからSequentialのインポート
from keras.models import Sequential
# keras.layersからDense、LSTMのインポート
from keras.layers import Dense, LSTM
# Dropoutのインポート
from keras.layers import Dropoutニューラルネットの構築や、パラメータのチューニング方法の説明は省略させて頂きますが、基本的な入力層、中間層と出力層からなるモデルをこのように構築することができます。また、このモデルをlstm_compという関数で定義しましょう。
# LSTM構築とコンパイル関数
def lstm_comp(df):
# 入力層/中間層/出力層のネットワークを構築
model = Sequential()
model.add(LSTM(256, activation='relu', batch_input_shape=(None, df.shape[1], df.shape[2])))
model.add(Dropout(0.2))
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(1, activation='sigmoid'))
# ネットワークのコンパイル
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
return model次に、作成したモデルが本当に予測に使用できるのかを確認する方法として、交差検証をしましょう。正解の分かっている学習データを複数に分割して、交差検証を行うのが有効です。
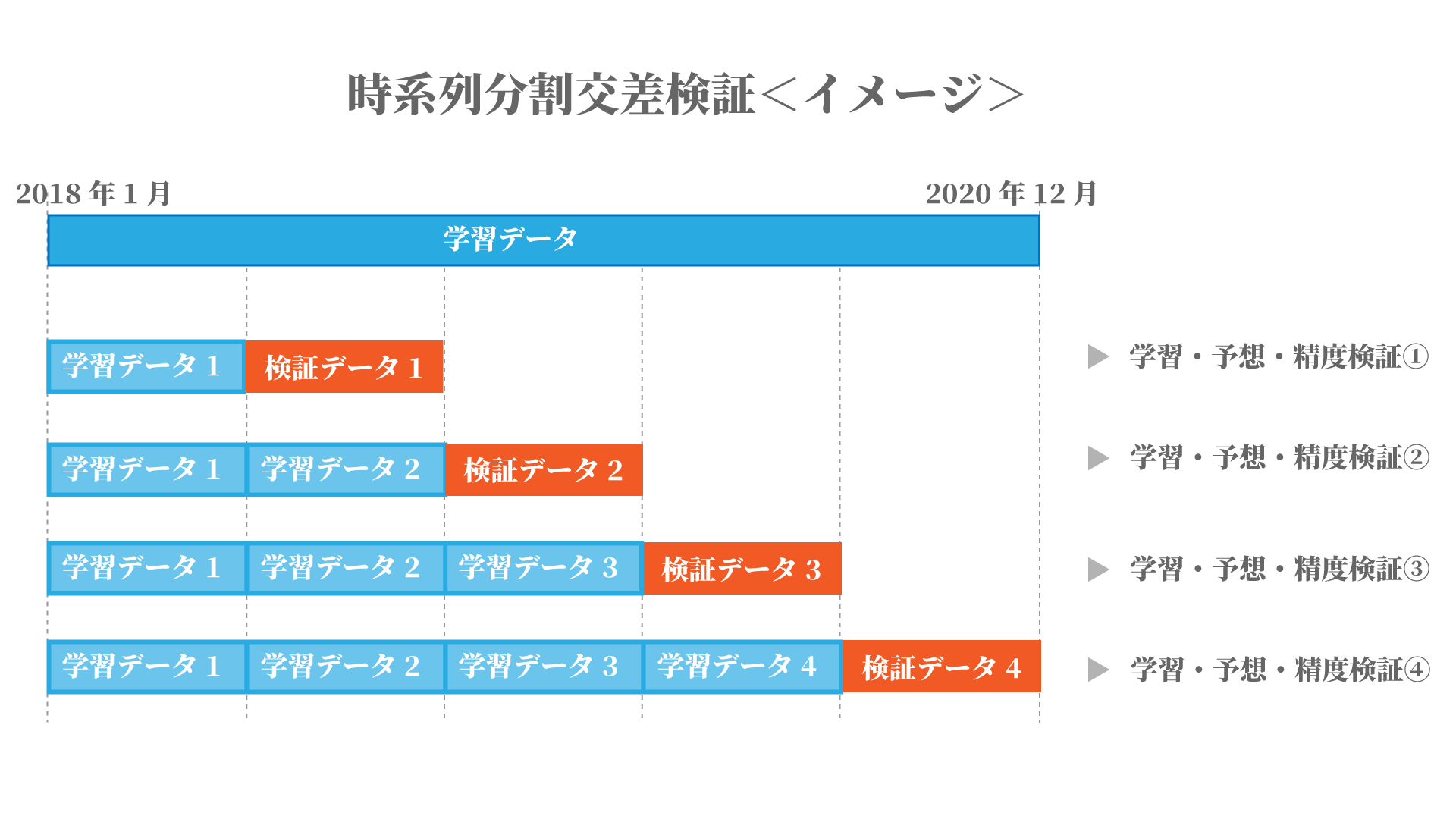
交差検証の手法には複数存在しますが、今回の様な時系列のデータで過去のデータを用いて未来を予測する場合は、時系列分割の交差検証を用いるのが一般的です。
今回は学習データを5分割し、学習データと検証データが図の様なイメージの組み合わせで合計4回の学習、予測と精度検証を繰り返します。これらのスコアの平均値から、モデルが予測に使用できるかの判断を行います。
この手法では検証データよりも過去のデータのみを用いて学習を行ないます。
まず、時系列分割交差検証を行うためのTimeSeriesSplitと、予測結果の精度(accuracy)を算出するためにaccuracy_scoreをインポートします。
# 時系列分割のためTimeSeriesSplitのインポート
from sklearn.model_selection import TimeSeriesSplit
# accuracy算出のためaccuracy_scoreのインポート
from sklearn.metrics import accuracy_scoreつぎに、4回分の交差検証の結果を代入する空のリストを作成します。そして、TimeSeriesSplitのインスタンス化を行い変数(tscv)に代入します。
valid_scores = []
tscv = TimeSeriesSplit(n_splits=4)for文を用いて、交差検証を4回繰り返します。
具体的にはこのような検証を実施します。
- splitメソッドを用いて学習データを分割し、交差検証用の学習データと検証データを作成
- 先に定義したlstm_comp関数よりLSTMモデルを作成
- 交差検証用の学習データより学習
- 検証データの説明変数を用いて予測
- 予測結果の2値化
- 検証データの目的変数(正解データ)を用いて、予測結果の精度算出と表示
- 予測精度のスコアをリストに格納
for fold, (train_indices, valid_indices) in enumerate(tscv.split(X_train_np_array)):
X_train, X_valid = X_train_np_array[train_indices], X_train_np_array[valid_indices]
y_train, y_valid = y_train_new[train_indices], y_train_new[valid_indices]
# LSTM構築とコンパイル関数にX_trainを渡し、変数modelに代入
model = lstm_comp(X_train)
# モデル学習
model.fit(X_train, y_train, epochs=10, batch_size=64)
# 予測
y_valid_pred = model.predict(X_valid)
# 予測結果の2値化
y_valid_pred = np.where(y_valid_pred < 0.5, 0, 1)
# 予測精度の算出と表示
score = accuracy_score(y_valid, y_valid_pred)
print(f'fold {fold} MAE: {score}')
# 予測精度スコアをリストに格納
valid_scores.append(score)
4回の交差検証が終了したら、予測精度のスコアが格納されたリストの表示し、スコアの平均値の算出と表示もしてみましょう。
4回のそれぞれのスコアと、平均値はこのようになりました。
print(f'valid_scores: {valid_scores}')
cv_score = np.mean(valid_scores)
print(f'CV score: {cv_score}')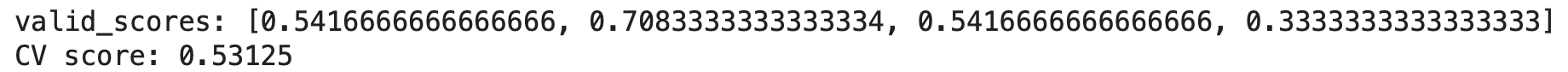
1回目:0.541
2回目:0.708
3回目:0.541
4回目:0.333
平均:0.531
今回のような上がるか下がるかの2値予測の場合、一般的にはスコアが0.5以上であればある程度使用できるという目安となります。
算出したスコアと平均値から、このモデルがある程度使用できるものと判断して次に進みましょう。
では、このモデルに対して、2018年から2020年の学習データを用いて学習をします。
流れは先ほどの交差検証と似ています。
まずは標準化した学習データでLSTMモデルを作成します。
# LSTM構築とコンパイル関数にX_train_np_arrayを渡し、変数modelに代入
model = lstm_comp(X_train_np_array)
作成したモデルで、学習します。
一瞬で学習が終了しました。
# モデルの学習の実行
result = model.fit(X_train_np_array, y_train_new, epochs=10, batch_size=64)今度は学習したモデルを用いて、検証データについて予測を行い、先頭の10個を表示させてみましょう。
# 作成したモデルより検証データを用いて予測を行う
pred = model.predict(X_val_np_array)
pred[:10]このように予測した結果が表示されます。
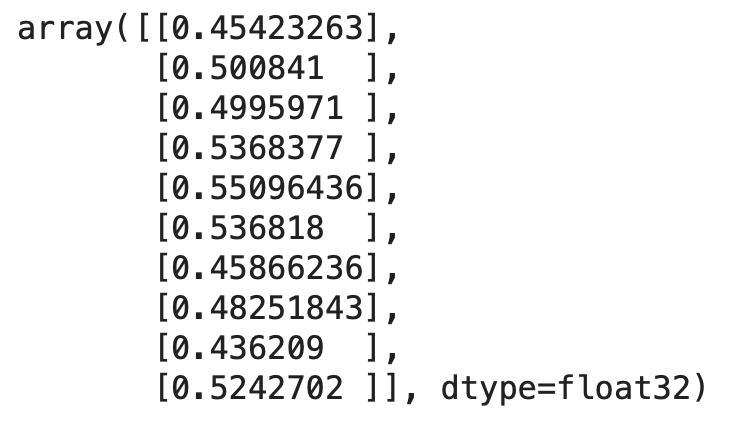
この数値を、上がるか下がるかの0と1に変換します。numpyのwhereメソッドを用いて0.5を超えるものを1、それ以外を0と修正します。そして再度先頭の10個を表示します。
これで、上がるか下がるかの01どちらかの予測ができました。
# 予測結果を0もしくは1に修正(0.5を境にして、1に近いほど株価が上昇、0に近いほど株価が上昇しない)
pred = np.where(pred < 0.5, 0, 1)
# 修正した予測結果の先頭10件を確認
pred[:10]
次に、予測モデルの精度確認を行います。この予測結果を実際の値となる検証データの目的変数と比較し、正解率を計算します。sklearnのaccuracy_scoreという関数を使うことで計算が行えます。
この結果を表示すると57%の正解率で有ることがわかります。今回の様な株価が上がるか下がるかの2値の予測では、直感的に予測を行う場合50%の正解率となります。機械学習を用いる事でそれを超える正解率となりました。
# 実際の結果から予測値の正解率を計算する
from sklearn.metrics import accuracy_score
print('accuracy = ', accuracy_score(y_true=y_val_new, y_pred=pred))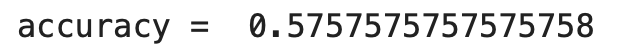
最後に、予測結果と正解結果を混同行列を用いて確認します。
混同行列とは、このように2行2列の表で、真陽性、真陰性、偽陽性、偽陰性の数を表したものです。今回は、予測が0で結果も0、予測が1で結果も1であれば正解です。0と予測して結果が1、1と予測して結果が0なら不正解ということになります。全体の精度だけではなく、0と1それぞれの正解に対する精度を確認することができます。
混同行列を生成するために、sklern.mericsからconfusion_matrixとConfusionMatrixDisplayをインポートします。
また、視覚的にわかりやすい様に、ヒートマップで表示しましょう。
このように、正しく予測が行えているのは、右下の真陽性(TP)と左上の真陰性(TN)です。予測結果が、0か1のどちらかに極端に偏っている傾向ではなさそうですが、正しく予測できていないものも存在していることがわかります。予測精度を改善することで、偽陽性(FP)と偽陰性(FN)の数を減らすことができます。
# 混同行列生成のためconfusion_matrixをインポート
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
# 混同行列を表示
cm = confusion_matrix(y_val_new, pred)
cmp = ConfusionMatrixDisplay(cm)
cmp.plot(cmap=plt.cm.Reds)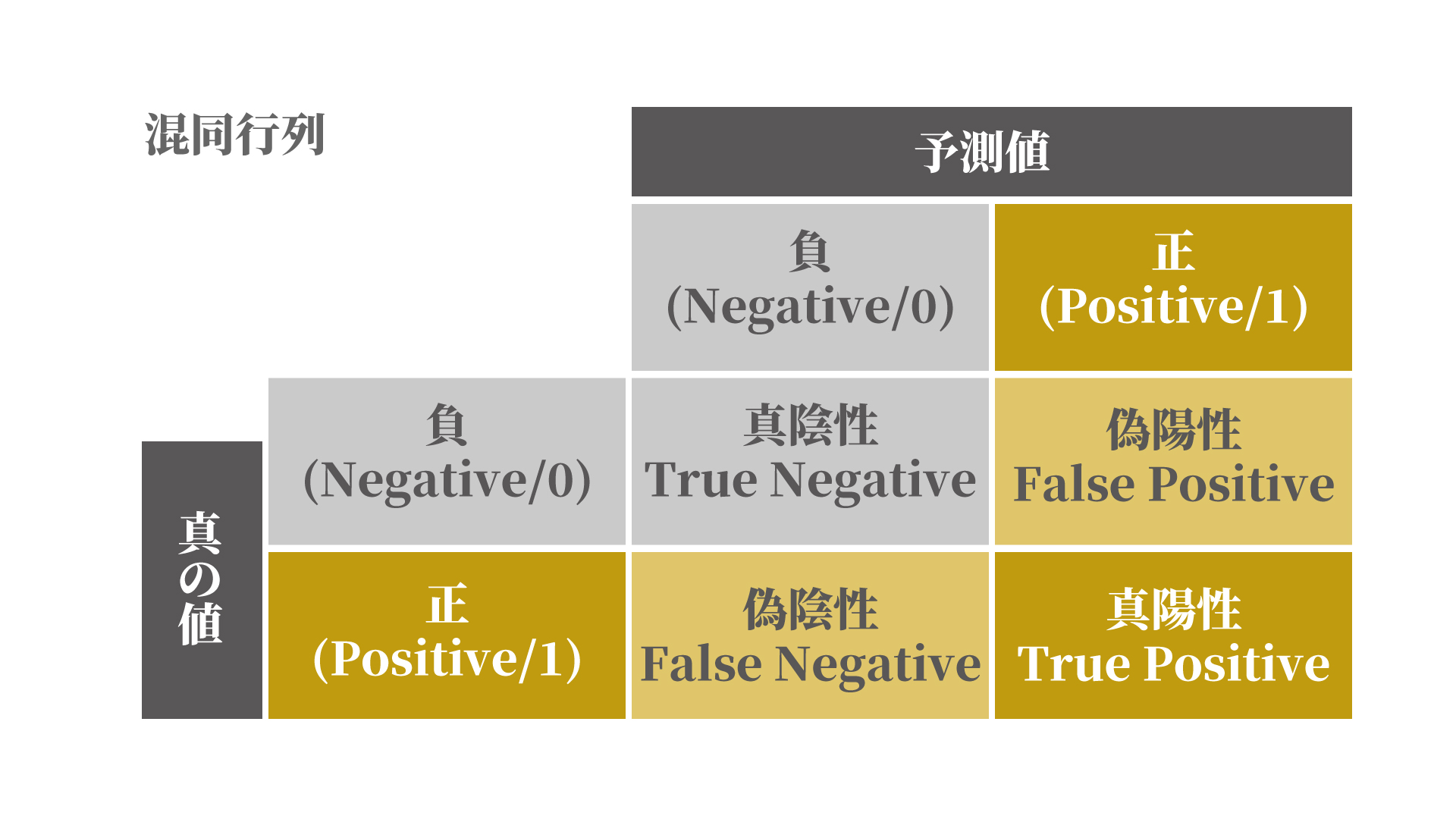
今回は基本的な特徴量や、機械学習モデルの構築方法で予測を行いました。特徴量を追加することや、学習モデルの改良を行うことで、予測精度を向上させることが可能です。
とはいえ、データの期間が変わるだけでも精度も変わります。必ずいつも予測がうまくいくわけではありませんのでご注意ください。
エンディング
いかがでしたでしょうか。
今後も、人工知能に関するレッスンをわかりやすく説明する動画の配信を予定しています。
レッスンの新着通知が⾏きますので、是⾮チャンネル登録をお願いします。
それでは、また次のレッスンでお会いしましょう。