重回帰分析〜ゼロからわかる理論編

はじめに

こんにちは、KinoCodeです。
お待たせしました。人工知能開発 入門講座、再開です。
人工知能開発、次のテーマとしまして、重回帰分析について説明します。
さて、これまでの動画を振り返ってみましょう。
1回目では、このコースの目的として、ビジネスマンが教養として人工知能を知ることの必要性を話しました。
2回目では、「人工知能とは何か？」というテーマで、用語の意味や、実際の活用事例など、人工知能の周辺知識について紹介しました。
3回目からは、具体的な手法として、単回帰分析について説明しました。
この人工知能開発入門講座では、1つの人工知能の手法に対して4回に分けて説明をします。
(1)数学がわからない方であっても概念を理解できる説明をする、「ゼロからわかる理論編」
(2)数学・統計学を使って概念の説明をする、数式を使って理解編。
(3)Excelを使って説明する、エクセルで学ぶ人工知能編。
(4)Pythonによる実装方法を説明する、Python実装編。
このような流れです。

この動画は、重回帰分析の1回目、「ゼロからわかる理論編」です。
数学が苦手な方でも理解できるよう、難しい理論は省きます。
つまり、ざっくりと「こういうものだ」と概論を理解いただけるように説明をします。
もっと詳しく理論を知りたい方は、次の数式を使って理解編もぜひご覧ください。

KinoCodeでは、人工知能開発に欠かせないPythonに関する動画をたくさん配信しています。
チャンネル登録がまだの方は、新着通知も届きますので、是非登録をお願いします。
それでは、レッスンスタートです。

重回帰分析とは

まず、重回帰分析の手法について説明します。
重回帰分析は単回帰分析と似ています。
単回帰分析は1種類の説明変数を使って量的データを予測する手法です。
対して重回帰分析は、2種類以上の説明変数を使って量的データを予測する手法です。
ここで、「量的データ」と言いましたが、ほかには「質的データ」があります。
量的データとは、身長や体重のように各データの大きさが比較できるデータを指します。
一方の質的データとは、男性や女性のように各データの大きさが比較できないデータのことを指します。
このような機械学習で使われる用語については、以前のレッスンで詳しく説明しています。
詳しく知りたい方、復習をしたい方はそちらをご覧ください。

では、住宅価格の予測を例にしてみましょう。
住宅価格を部屋の数という1つの説明変数だけを使って予測するのが単回帰分析です。
一方、部屋の数の他に駅からの距離、築年数など、複数の説明変数を使って予測するのが重回帰分析です。
重回帰分析は説明変数が複数あるだけで、分析の流れは単回帰分析と同じです。
単回帰分析の復習も兼ねて、一緒に学んでいきましょう。

重回帰分析の概要

それでは、重回帰分析の概要について説明します。
今回は説明変数が2種類の場合について説明しますが、3種類以上の場合も同様です。
このような住宅価格のデータを使用します。

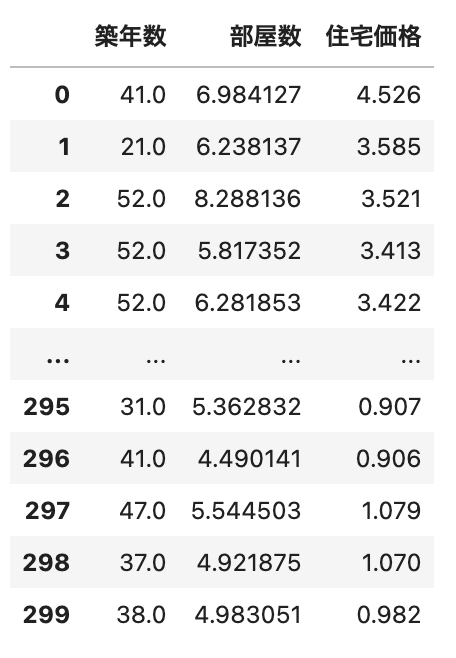
築年数はある地区の住宅の築年数の中央値、部屋数はその地区の住宅の平均の部屋数、住宅価格はその地区の物件の中央値を表しています。
住宅価格の単位は10万ドルです。
この、築年数と部屋数から、住宅価格を予測するものとしましょう。
つまり、築年数と部屋数が説明変数、住宅価格が目的変数です。
では、関係性を見るために、グラフにしてみましょう。
x軸を築年数、y軸を部屋数、z軸を住宅価格として、このデータを3次元のグラフにプロットするとこのようになります。

3次元のプロットは少し見づらいので、角度を変えて表示します。

一番左のグラフは、3次元のプロットを部屋数側から見たときのグラフです。
z軸を中心に45度左回りに回転させたグラフが真ん中のグラフです。
そして、z軸を中心にさらに45度左回りに回転させ、3次元のプロットを築年数側から見たときのグラフが一番右のグラフです。
このグラフを見ると、部屋数が多いほど住宅価格は高くなっていそうです。
また、若干ではありますが築年数が高いほど住宅価格は低くなっていそうな気がします。
この関係性がわかれば、住宅価格が求められそうですよね。
この部屋数、築年数と住宅価格の関係式を求め、未知の住宅価格を予測するのが重回帰分析です。

ではどのように関係式を求めるのでしょうか？
単回帰分析では最小二乗法という手法を使いました。
最小二乗法とは、できるだけデータの近くを通るような直線を求める手法です。これを用いて、関係式を求めました。
重回帰分析でも、同じように最小二乗法を使って、できるだけデータの近くを通るような関係式を求めます。
ただし、説明変数が2種類あります。よって、求めるのは直線ではなくこのような平面になります。

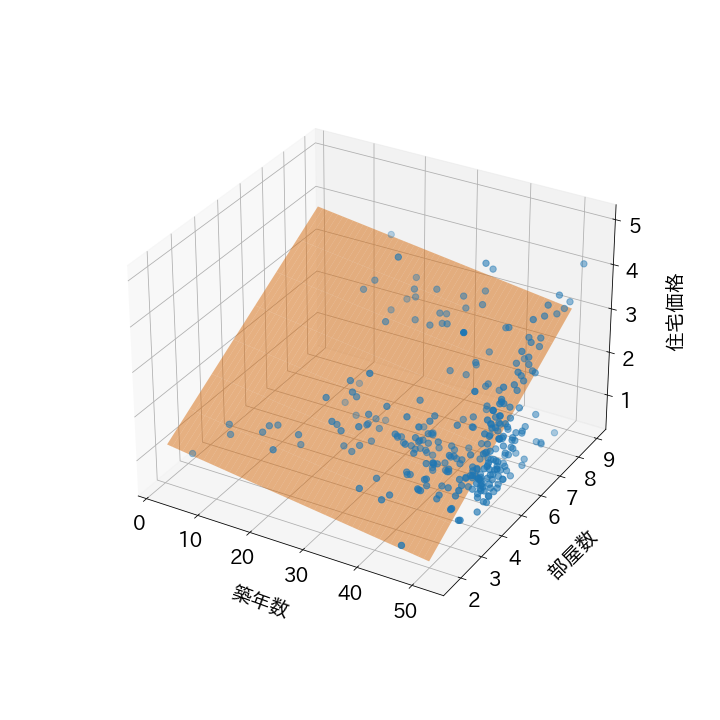
こちらも角度を変えて表示してみましょう。

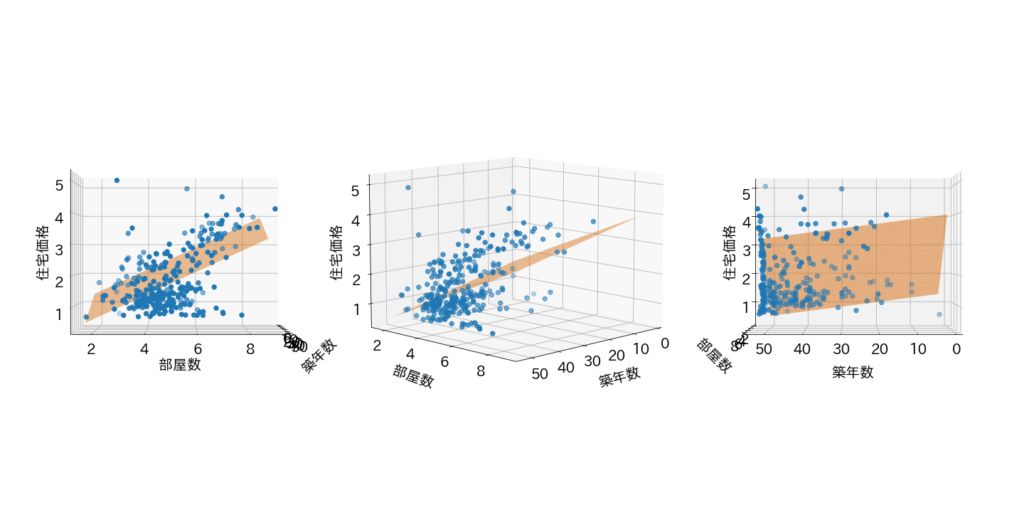
先ほどと同様に、一番左のグラフが3次元のグラフを部屋数側から見たときのグラフです。
z軸を中心に45度左回りに回転させたグラフが真ん中のグラフです。
そして、z軸を中心にさらに45度左回りに回転させ、築年数側から見たときのグラフが一番右のグラフです。
この平面上の点は、部屋数が多いほど住宅価格は高くなり、築年数が高いほど住宅価格は低くなっています。3つの関係を表していそうです。
そしてこのような平面の関係式を導出します。
関係式がわかれば、築年数と部屋数から住宅価格を予測できそうですね。
例えば、築年数が40で部屋数が2の場合はどうでしょう。住宅価格は約0.8万ドルと予測できます。
例えば、築年数が20で部屋数が4の住宅価格はどうでしょう。約2万ドルと予測できます。
こうして関係式を求めて予測する手法を重回帰分析といいます。

ちなみに、重回帰分析は説明変数が2種類以上あるだけで、分析手法は単回帰分析とほとんど同じです。
最小二乗法を使ってできるだけデータの近くを通るような平面を求め、関係式を導出します。
そしてその関係式から、未知の目的変数の値を予測するという手法です。
また、今回は説明変数が2種類の場合について説明しました。
説明変数が3種類以上ある場合も、最小二乗法を使って超平面と呼ばれる空間を求め、関係式を導出します。
ただし、グラフに表せないのでイメージしづらいです。
とはいえ、分析手法は説明変数が2種類の場合と全く同じです。
実際の業務において、説明変数が多く存在することも少なくありません。
説明変数が複数ある場合に使用することができる分析手法のひとつであることを覚えておきましょう。

おわりに

今回のレッスンは以上です。重回帰分析の概要は理解できましたでしょうか？
概要を掴むことができたら、早速実装してみるのもひとつの手段です。
Excelで学ぶ人工知能編、Pythonで実装編に進んでみてください。
もっと理論を学習したい人は、次の「数式を使って理解編」をご覧ください。
チャンネル登録と新着通知を忘れずにお願いします。
それでは次の動画でお会いしましょう。